Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-22T04:53:14.214Z Has data issue: false hasContentIssue false
  • English
  • Français

Recursive averages and the renewal theorem

Published online by Cambridge University Press:  12 November 2024

G. J. O. Jameson
G. J. O. Jameson*
Affiliation:
13 Sandown Road, Lancaster LA1 4LN e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the sequence of numbers an defined by the iteration (1)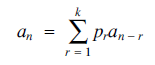 for n ≥ k, where pr 1 ≤ r ≤ k) are non-negative numbers with 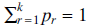and the starting values are given. So an is a weighted average of the previous k terms.

Type
Articles
Information
The Mathematical Gazette , Volume 108 , Issue 573 , November 2024 , pp. 437 - 449
Check for updates
Copyright
© The Authors, 2024 Published by Cambridge University Press on behalf of The Mathematical Association

References

Flanders, H., Averaging sequences again, Math. Gaz. 80 (July 1996) pp. 219-222.CrossRefGoogle Scholar
Lord, N., Sequences of averages revisited, Math. Gaz. 95 (July 2011) pp. 314-317.CrossRefGoogle Scholar
Rohan Manojkumar Shenoy, The discrete renwal theorem with bounded inter-event times, Math. Gaz. 107 (July 2023) pp. 343-348.CrossRefGoogle Scholar
Sanders, P., Averaging sequences, Math. Gaz. 78 (November 1994) pp. 326-328.CrossRefGoogle Scholar
Feller, W., An introduction to probability theory and its applications, Wiley (1971).Google Scholar
Lotka, A. J., A contribution to the theory of self-renewing aggregates, with special reference to industrial replacement, Ann. Math. Stats. 10 (1939) pp. 1–25.CrossRefGoogle Scholar
Keyfitz, N., Introduction to the mathematics of population, Addison-Wesley (1968).Google Scholar
Apostol, T. M., Mathematical analysis, Addison-Wesley (1957).Google Scholar
Bachman, G. and Narici, L., Functional analysis, Academic Press (1966). Google Scholar