Article contents
On Von Staudt’s Geometrie der Lage
Published online by Cambridge University Press: 03 November 2016
Extract
The extent of the complete domain can be estimated by comparing it with its real part, that is, with the visible universe. For the sake of this comparison, von Staudt speaks as though it were possible to specify the number of real elements in any base, but gives an explicit warning as to the meaning he attaches to the symbol n which he uses for an infinitely great quantity. The number of real points on a line he denotes by n + 1; the one is apparently the ideal point, the n belonging to the actual universe. Now every imaginary pair can be assigned by means of a harmonic cast with one point, A, fixed. If this be (ABA′B′), we have a choice of 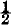 n(n − 1) pairs for BB′, but no further choice; the number of imaginary points is therefore 2 ×
n(n − 1) pairs for BB′, but no further choice; the number of imaginary points is therefore 2 × 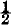 n(n−1), that is, n(n−1). Hence if the number of real points on a line is denoted by n+1, the total number of points on the line is n2+1. On an imaginary line of the first kind the points are one real, n imaginary; on an imaginary line of the second kind all are imaginary.
n(n−1), that is, n(n−1). Hence if the number of real points on a line is denoted by n+1, the total number of points on the line is n2+1. On an imaginary line of the first kind the points are one real, n imaginary; on an imaginary line of the second kind all are imaginary.
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 1900
- 3
- Cited by


