No CrossRef data available.
Article contents
On the Multiplication of Complex Numbers
Published online by Cambridge University Press: 03 November 2016
Extract
In the development of the theory of complex numbers, it is important to give a definition of them dependent only upon real numbers. In the usual algebraic treatments the product is postulated in the form
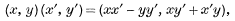
or obtained from a matrix representation. The object of the present note is to show by elementary methods that the assumption that the multiplication of complex numbers is distributive, associative, and such that the vanishing of a product implies the vanishing of at least one factor, is sufficient to define the product. This is indeed merely a special case of results well known in the theory of linear algebras.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Mathematical Association 1949


