Article contents
On the Inversion Property of the Mobius’ μ-Function
Published online by Cambridge University Press: 03 November 2016
Extract
Mobius‘ function has the important property of inverting functional relations [1] of the type
 and
and
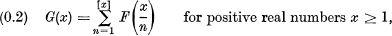 giving in turn
giving in turn
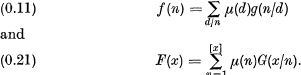 (Also relations (0.1) and (0.2) follow respectively from (0.11) and (0.21))
(Also relations (0.1) and (0.2) follow respectively from (0.11) and (0.21))
I establish in this paper that no other arithmetical function μ*(n) can perform the above inversion. In other words, I prove that Inversion is the characteristic property of Mobius‘ μ-function. Theorem 1 below asserts that if for one pair of functions g(n) and f(n) (subject to a special condition) relations (0.1) and (0.11) are true with an arithmetical function μ*(n) (possibly depending on g and f), then μ*(n) coincides with the Mobius‘-function. Theorem 2 below gives a similar result in connection with functions G(x) and F(x) defined for all real x ≥ 1.
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 1963
References
- 4
- Cited by


