No CrossRef data available.
Article contents
On Higher Trigonometry: III. The Elementary Transcendental Fuctions
Published online by Cambridge University Press: 03 November 2016
Extract
The following system of algebraic inequalities is of great value and of wide application:

for all positive proper fractional values of a,
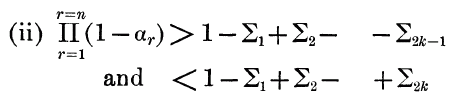
for positive proper fractional values of α1, α2, αn, and value of k Such that 2k<n; ∑r denoting the sum of the r-products of the α’s.
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 1906
References
Page 359 of note * The student need not up to this stage have given any attention to the theory of infinite series; he will probably have had his attention drawn to the geometric infinite series and its application to recurring decimals.
Page 360 of note * If need is felt for further satisfaction, reference can be made to Chrystal, chap, xxv., § 13, where it is proved that the function (l + l/x)x increases steadily when an increasing system of positive rational values is given to x. Also to Harnack’s Introduction to the Calculus, Bk. I., ch. vi., § 28, or to Gibson’s Calculus, ch. v., § 48. But some assumption similar in type to that suggested above must always be implicitly made; cp. footnote p. 332, Gazette, July, 1906.
Page 361 of note * The device used here looks as if it might have a wide application; it is again applied to the Infinite Products. See p. 362.
Page 363 of note * Cp. p. 360 of this number.
Page 364 of note * For another method of establishing these results, see a paper by the writer of this article in the Proc. Edin. Math. Soc., vol. xxii.; the treatment there is of the real case, but the analysis is suggestive in the present connection and instructive to the beginner.


