No CrossRef data available.
Article contents
On a sequence of algebraic formulae of Ramanujan
Published online by Cambridge University Press: 23 January 2015
Extract
Among the many astonishing formulae stated by Ramanujan we find in his Notebooks the following sequence (see [1], p 96, Entry 43):
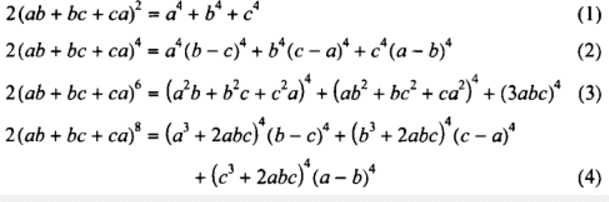
which hold for any triple of complex numbers (a, b, c) such that a + b + c = 0.
Ramanujan concluded this list by ‘And so on’, which suggests that he had some kind of method or algorithm allowing him to extend this list to any even power of the quadratic form p(a, b, c) = ab + bc + ca, when a + b + c = 0. To explain this, Bruce Brendt details a theorem by S. Bhargava [2], which can be used to produce identities of the kind above, and infers that Ramanujan is likely to have used the same proof to establish his identities (see [1], pp. 97-100)
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 2012
References
1.
Berndt, Bruce, Ramanujan notebooks, Part IV, Springer Verlag, New York (1994).CrossRefGoogle Scholar
2.
Bhargava, S., On a family of Ramanujan's formulas for sums of fourth powers, Ganita
43 (1992) pp. 63–67 (as quoted in [1]).Google Scholar