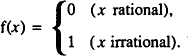Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-12-02T19:09:31.516Z Has data issue: false hasContentIssue false
  • English
  • Français

Modelling irrational numbers in analysis using elementary programming

Published online by Cambridge University Press:  01 August 2016

David Tall  and
John Mills
David Tall
Affiliation:
Mathematics Education Research Centre, University of Warwick, Coventry, CV4 7AL
John Mills
Affiliation:
Mathematics Education Research Centre, University of Warwick, Coventry, CV4 7AL
Get access Rights & Permissions [Opens in a new window]

Extract

In recent years we have been teaching mathematical analysis using the computer to give experiences to help students understand the concepts [1]. It has proved to be a valuable aid in many ways, but the method depends on giving a suitably rich environment enabling students to experience the full range of possibilities. A great weakness of the use of regular computer languages is that they hold numbers in memory as a finite expansion in base two, so, effectively, all numbers in such a system are rational. This meant that we were unable to demonstrate any ideas that depend on the difference between rationals and irrationals; for instance, we could not plot graphs of the kind

Type
Research Article
Information
The Mathematical Gazette , Volume 76 , Issue 476 , July 1992 , pp. 243 - 250
Copyright
Copyright © The Mathematical Association 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Mills, J., and Tall, D.O., “From the visual to the logical”, Bulletin of the I.M.A., 24 (11/12), P 176–183 (1988).Google Scholar
2. Mathematical Association, 132 short programs for the mathematics classroom, Stanley Thornes (1985).3. Tall, D.O., Real functions and graphs, C.U.P., (software for the BBC, Nimbus and Archimedes. The special facilities in this article are currently implemented only on the Archimedes, using its considerably greater speed.) (1991).Google Scholar
3. Mills, J., and Tall, D.O., “From the visual to the logical”. Bulletin of the IMA. 24 (11/ 12) 176–183.Google Scholar
4. Weir, A.J., General integration and measure, C.U.P., (1973).Google Scholar