No CrossRef data available.
Article contents
Linearly periodic continued fractions
Published online by Cambridge University Press: 13 October 2021
Extract
An infinite simple continued fraction representation of a real number α is in the form
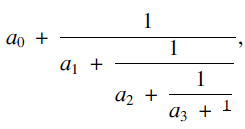 $$\eqalign{& {a_0} + {1 \over {{a_1} + {1 \over {{a_2} + {1 \over {{a_3} + {1 \over {}}}}}}}} \cr & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots \cr} $$
$$\eqalign{& {a_0} + {1 \over {{a_1} + {1 \over {{a_2} + {1 \over {{a_3} + {1 \over {}}}}}}}} \cr & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots \cr} $$
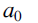 $${a_0}$$
is an integer, and
$${a_0}$$
is an integer, and 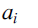 $${a_i}$$
are positive integers for
$${a_i}$$
are positive integers for 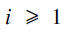 $$i \ge 1$$.
This is often written more compactly in one of the following ways:
$$i \ge 1$$.
This is often written more compactly in one of the following ways:
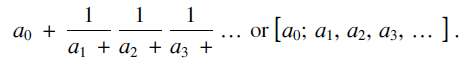 $${a_0} + {1 \over {{a_1} + }}{1 \over {{a_2} + }}{1 \over {{a_3} + }} \ldots \;{\rm{or}}\;\left[ {{a_0};\;{a_1},\;{a_2},\;{a_3} \ldots } \right]$$
$${a_0} + {1 \over {{a_1} + }}{1 \over {{a_2} + }}{1 \over {{a_3} + }} \ldots \;{\rm{or}}\;\left[ {{a_0};\;{a_1},\;{a_2},\;{a_3} \ldots } \right]$$
- Type
- Articles
- Information
- Copyright
- © The Mathematical Association 2021



