Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-12-03T19:11:28.722Z Has data issue: false hasContentIssue false
  • English
  • Français

Identities connecting the Chebyshev polynomials

Published online by Cambridge University Press:  17 October 2016

Jonny Griffiths
Jonny Griffiths*
Affiliation:
20 Rosebery Road, Norwich NR3 3NA e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

There are many families of polynomials in mathematics, and they often occur naturally in pairs. The Fibonacci polynomials and the Lucas polynomials, for example, are generated by the same recurrence relation but with different starting values, and there are many identities that link the two families [1]. The same is true for the Chebyshev polynomials of the first and second kinds, Tn (x) and Un (x) [2], respectively. There are two further polynomial families that are less well-known, the Chebyshev polynomials of the third and fourth kinds, Vn (x) and Wn (x) [3], respectively. Each of the four kinds is an example of an orthogonal polynomial family Pn (x), where for some appropriate weight function W (x), 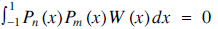whenever n ≠ m. The families Tn (x) and Un (x) in particular are ubiquitous in their mathematical uses, in approximation theory, in differential equations, and in solving the Pell equation, to name but three. There are also many connections between Tn (x), Un (x), Vn (x) and Wn (x), some of which are explored here, and some of which we hope are new.

Type
Articles
Information
The Mathematical Gazette , Volume 100 , Issue 549 , November 2016 , pp. 450 - 459
Copyright
Copyright © Mathematical Association 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Wikipedia, Fibonacci Polynomials, accessed February 2016 at http://en.wikipedia.org/wiki/Fibonacci_polynomials Google Scholar
2. Wikipedia, Chebyshev Polynomials, accessed February 2016 at http://en.wikipedia.org/wiki/Chebyshev_polynomials Google Scholar
3. Mason, J. C., Factorisation properties of Chebychev polynomials, Mathematics 49, (December 1993) pp. 169–178.Google Scholar
4. The On-line Encyclopedia of Integer Sequences, accessed February 2016 http://oeis.org Google Scholar
5. Griffiths, J., Lyness Cycles, Hikorski Triples and Elliptic Curves, MSc Thesis, University of East Anglia (2012), accessed February 2016, also available at http://www.s253053503.websitehome.co.uk/jg-msc-uea/index.html Google Scholar
6. Rayes, M., Trevisan, V., and Wang, P., Factorisation properties of Chebychev polynomials, Comput. Math. Appl. 50 (2005) pp. 1231–1240.Google Scholar