No CrossRef data available.
Article contents
Groups, conics and recurrence relations
Published online by Cambridge University Press: 03 July 2023
Extract
In this paper we explore some of the geometry that lies behind the real linear, second order, constant coefficient, recurrence relation(1)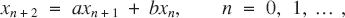 where a and b are real numbers. Readers will be familiar with the standard method of solving this relation, and, to avoid trivial cases, we shall assume that ab ≠ 0. The auxiliary equation of t2 = at + b of (1) has two (possibly complex) solutions
where a and b are real numbers. Readers will be familiar with the standard method of solving this relation, and, to avoid trivial cases, we shall assume that ab ≠ 0. The auxiliary equation of t2 = at + b of (1) has two (possibly complex) solutions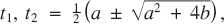 and the most general solution of (1) is given by
and the most general solution of (1) is given by
(i)
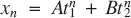 when
when 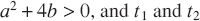 are real and distinct;
are real and distinct;(ii)
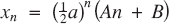 when
when 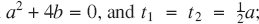
(iii)
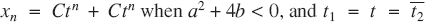
- Type
- Articles
- Information
- Copyright
- © The Authors, 2023. Published by Cambridge University Press on behalf of The Mathematical Association



