Hostname: page-component-7bb8b95d7b-fmk2r Total loading time: 0 Render date: 2024-09-06T13:42:20.240Z Has data issue: false hasContentIssue false
  • English
  • Français

Fractional Calculus

Published online by Cambridge University Press:  03 November 2016

W. Fabian
Get access Rights & Permissions [Opens in a new window]

Extract

We continue here our work on fractional integration and differentiation of functions of a real variable which we began in a previous paper. All quantities in the present paper are real.

We define a λth integral, or a (−λ)th differential coefficient, of f(x) over an interval (a, x)by

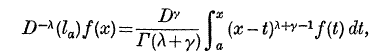
where D stands for 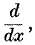and γ is the least integer greater than or equal to zero such that λ + γ>0, f(x) is bounded on the path of integration, and is continuous on this path except possibly for a finite number of ordinary discontinuities.

Type
Research Article
Information
The Mathematical Gazette , Volume 21 , Issue 244 , July 1937 , pp. 216 - 219
Copyright
Copyright © Mathematical Association 1937

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Page no 216 note * Fabian, , Math. Gazette, vol. 20 (1936), pp. 88–92. In our other previous papers on the Fractional Calculus the complex variable was used.CrossRefGoogle Scholar

Page no 218 note * Fabian, , Phil. Mag. vol. 20 (1935), pp. 781–789.CrossRefGoogle Scholar

Page no 218 note † Fabian, , Math. Gazette, vol. 20 (1936), pp. 88–92.CrossRefGoogle Scholar

Page no 219 note * Fabian, , Math. Gazette, vol. 20 (1936), pp. 88–92.CrossRefGoogle Scholar