No CrossRef data available.
Article contents
Farey rabbits
Published online by Cambridge University Press: 01 August 2016
Extract
The Farey sequence of order n(Fn) is the sequence of all reduced fractions between 0 and 1, whose denominator does not exceed n, arranged in increasing order of magnitude.
For example, F6 is 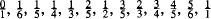 .
.
The Fibonacci sequence is the sequence for which u1 = 1, u2 = 1 and un = un-1 + un-2,namely, 1, 1, 2, 3, 5, 8, 13, … , un
At first sight, there is little connection between Farey’s fractions and Fibonacci’s integers. The purpose of this note is to show and explore such a connection and hence derive some properties of the Fibonacci sequence directly from previously proved properties of the Farey sequences. The former properties are well-known, but their rather unusual derivation from Farey properties may have some interest.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Mathematical Association 2000


