Article contents
The Exponential and Logarithmic Functions
Published online by Cambridge University Press: 03 November 2016
Extract
The usual method of developing the theory of the exponential and logarithmic functions is to take as a definition either
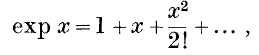
or 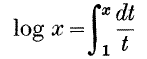
The first definition has the disadvantage that with it a good deal of the theory of series is needed. Neither development follows the lines on which the student first met the functions. A good deal could be said for the view that for most students the best type of accurate theory is one which fills up the gaps in methods which are already familiar The difficulties of taking
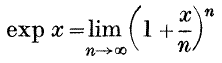
as a definition are well known.
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 1936
References
page no 258 note * See H. G. Forder, Foundations of Euclidean geometry (1927).
page no 258 note † See G. H. Hardy, Pure Mathematics, p. 139, or Hardy, Littlewood and Pól;ya, Inequalities, Th. 41, p. 39. These are referred to as P.M. and H.L.P. respectively.
page no 259 note * The obvious extension has “≤” in place of “<”, but this is enough for our purpose. For the extension with “<” see H.L.P., p. 41, or use methods suggested on p. 18 of H.L.P.
page no 259 note † We have used the rule ![]()
page no 260 note * In P.M. (5th ed., p. 387) these are based on a definition of 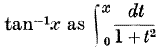 The method here avoids the infinities of tan x and enables us to use Euler’s beautiful proof of the addition theorem.
The method here avoids the infinities of tan x and enables us to use Euler’s beautiful proof of the addition theorem.
page no 260 note † C(x) and finite because, if 0≤x≤1–2−n ,

page no 261 note * The verification of the derivatives is almost trivial except at multiples of ½Π, and here is much simpler than if our basis were tan−1 x, as we do not have to deal with the infinities of tan x.
page no 262 note * We have defined and use only the principal value of log z.
page no 262 note † The error term is the sum of a finite number of terms each of the form
O(|x| r |y| s ) where n + 1 ≤ r + s ≤ 2(n + 1).
- 1
- Cited by


