No CrossRef data available.
Article contents
A digit function with Thomae-like properties
Published online by Cambridge University Press: 23 January 2015
Extract
Following a recent revival of interest in both Thomae's function and digit functions (see [1] and [2] respectively) we present here a function providing an appealing link between the two. The former, nowadays often cited in courses on real analysis, was given by Thomae in 1875; see also [3], [4] and [5]. This function, which we denote by g(x), has the following definition:
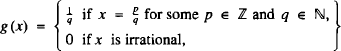
where it is so be assumed that gcd (p, q) = 1 when x is rational.
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 2011
References
1.
Beanland, K., Roberts, J. W., and Stevenson, C., Modification of Thomae's function and differentiability, Amer. Math. Monthly
116 (2009) pp.531–535.Google Scholar
2.
Simons, S., Summing digits of an arithmetic sequence, Math. Gaz.
92 (2008) pp. 83–86.Google Scholar
4. Wikipedia: The Free Encyclopedia, Thomae's function, http://en.wikipedia.org/wiki/Thomae's_function
Google Scholar
5.
Wilcox, H. J. and Myers, D. L., An introduction to Lebesgue integration and Fourier series, Dover (1995) p. 8.Google Scholar
6.
Drmota, M. and Gaidosik, J., The distribution of the sum-of-digits function, Journal de Théorie des Nombres de Bordeaux
10 (1998) pp.17–32.Google Scholar
7.
Kirschenhofer, P., On the variance of the sum of digits function, Lecuture Notes Math.
1452 (1990) pp.112–116.Google Scholar


