No CrossRef data available.
Article contents
Conics twinned with two special circles
Published online by Cambridge University Press: 23 January 2015
Extract
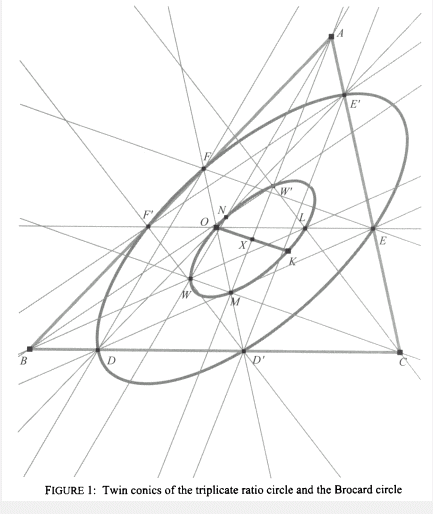
Throughout the article we use areal (or barycentric) coordinates. The side lengths of BC, CA, AB are denoted as usual by a, b, c and for brevity and ease of reading we write a2 = p, b2 = q, c2 = r. The symmedian point K then has coordinates (a2, b2, c2 ) replaced by (p, q, r), it being the isogonal conjugate of the centroid, and the circumcentre O then has coordinates (a2(b2 + c2 − a2), b2(c2 + a2 − b2), c2(a2 + b2 − c2)) replaced by (p(q + r − p), q(r + p − q), r(p + q − r)). The construction of the triplicate ratio circle (also known as the Lemoine circle) and the Brocard circle is replicated but starting with the circumcentre O rather than the symmedian point K. It is found that the triplicate ratio circle is then replaced by a conic cutting internally each side of ABC twice and having centre X the midpoint of OK. The Brocard circle is replaced by a conic passing through O and K and also having centre X the midpoint of OK. These we define as the twin conics.
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 2012


