Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-11T22:14:20.556Z Has data issue: false hasContentIssue false
  • English
  • Français

A Condition for Right-Angled Triangles

Published online by Cambridge University Press:  03 November 2016

B. D. Price
Get access Rights & Permissions [Opens in a new window]

Extract

IT is well known that the identity

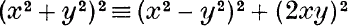
enables one to generate right-angled triangles with integral sides merely by putting x and y as integers (x>y). It is sufficient that x, y be integers, to give a right-angled triangle with hypotenuse x2+y2 and sides x2—y2, 2xy. Is the condition necessary? No, for the triangle with sides 9, 12, 15 (a multiple of the 3, 4, 5 case) cannot be expressed by the above identity without using surds. VVe will, however, prove the following proposition:

Type
Research Article
Information
The Mathematical Gazette , Volume 33 , Issue 304 , May 1949 , pp. 121 - 122
Copyright
Copyright © Mathematical Association 1949

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)