No CrossRef data available.
1,1. This contribution to a fundamentally important subject has a multiple origin. Its immediate occasion is the address by Professor Temple, on “The Theory of Complex Numbers”, published in the Gazette of July 1937; and its theme is another alternative to the two types of “theory” there considered (“descriptive” and “constructive”)—which may be designated descriptive-in-terms-of-discovery.
page no 225 note * Its deeper origin is a lifework of teaching, rooted in direct study of “Number”, as a mathematical phenomenon. At a certain stage of its development, the results of that study were published in a little book: The Number-System of Arithmetic and Algebra (Melb. Univ. Press). That book was somewhat severely criticised in the Gazette (XVIII, 231, p. 359): making evident the fact that it had failed to convince a highly competent reviewer. Consequent correspondence with that reviewer stimulated fruitful revision and development of the presentation of the case. This was partly represented in a paper to Section A of the Australasian Association for the Advancement of Science (Auckland, N.Z., Jan. 1937)—not offered for publication to that body. The work of revision—and completion—has been finished during 1937.
This present paper (it seems necessary to add) is to be regarded as a personal contribution to a difficult (and even controversial) subject.
page no 225 note † Thus Dedekind, in his famous essay on “Continuity and Irrational Numbers”, says “negative and fractional numbers have been created by the human mind” (p. 4); and, again, in a section headed “Creation of Irrational Numbers”, he says “...we create a new, an irrational number...” (p. 15) (Open Court Publishing Co.’s translation (1901) of Essays on Number by Dedekind). It seems to be highly important to distinguish between what we “create” (or “invent”) and what we “discover”. In Mathematics we create modes and forms of expression, and invent technique.
page no 225 note ‡ The “pure vector”, of standard Vector Analysis, is most simply conceived as being constituted of “a real number” and a direction.
page no 225 note § Vide § 6, infra.
page no 226 note * Elsewhere—throughout Physical Science—the “operator” alone is a “number”: the two other quantities, involved in the “operation”, being of some other kind (vide, e.g., § 4, 2 infra). On the other hand, of course, an “operator” —even in Pure Mathematics—is not necessarily a “number”.
page no 226 note † Vide § 3, infra.
page no 226 note ‡ Here, the context of “commonsense approach” is essential to the argument. The endeavour is to deal with “number”, carefully and accurately, as it has been discovered—for use by scientific workers in its highly important applications. This leaves untouched the logical and philosophical discussion of the number concept —though it is by no means irrelevant to that discussion.
The view may be taken that “commonsense” requires only one category; but that would surely be mistaken—seeing that there is much real and practical knowledge of the numbers of “counting”, quite unassociated with any other adequate knowledge of “number”—also that, even among the educated, knowledge of “numbers” of any other kind is still so hazy (as indicated by common use of such terms as “fraction” and “minus quantity”). See also § 2, 2, with footnote.
page no 226 note § “Complex Number” is generally used in such a way as to be inclusive of all the “numbers” of this second category. The general question of the terminology of “Number”, in mathematical theory, is one for critical discussion—not coming within the scope of this paper.
page no 226 note ‖ It is rooted in the distinction, from this point of view, between the Natural Numbers and “the positive integral numbers”. Vide § 3, 3 and § 6, 3, infra.
page no 227 note * Dedekind (loc. cit.) says: “I regard the whole of arithmetic as a necessary, or at least a natural, consequence of the simplest arithmetical act, that of counting . . .” (p. 4). This—somewhat abstracted from its context—is the view here taken of the arithmetic of the Natural Numbers.
(Dedekind’s view of the significance of “measurement” is a good deal different from that expressed in this treatment. He was so intent on his share in the great pioneering work in one direction—“that arithmetic shall be developed out of itself” (loc. cit., p. 10)—that he seems to have missed some of its implications in the opposite direction. His insistence on “creation” of numbers by the human mind” (vide footnote to § 1, 1, supra), and his incidental references to “the complex numbers” (loc. cit., p. 10), are highly significant. The present writer—who owes more to the inspiration of that one essay than to any other single source— indicates his own view on these points in §§ 6 and 7, infra.)
page no 227 note † It is, of course, possible to make a logical analysis of these basic facts about Addition of the Natural Numbers.
page no 227 note ‡ E.g. 23 = 8, 32 = 9; (23)4 = 212, 2(34 ) = 281; also (33)3 = 39, 3(33 ) = 327.
page no 227 note § Also Division—especially when combined with Subtraction in “the Division-transformation”.
page no 228 note * The curious thing is that Logarithmation is not usually dealt with at this stage—where the relevant facts are quite simple and elementary—although the general mathematical operation of Logarithmation (unlike the other operations) is of no particular significance again, until the stage of the “Real Numbers”, where all the relevant facts are peculiarly difficult. The interesting section on “Logarithms” in the Math. Assoc. Report on the Teaching of Arithmetic should be looked at from this point of view.
page no 228 note † The standard notation for the last two of the seven operations is not quite good enough. There is more than one possibility for the last three; but, retaining ab (as, probably, the best possible form) for Involution (Potentiation), the other two might with advantage be simplified to
ba and
ba, respectively, for Evolution (Radication) and Logarithmation vice
![]() and log
ba.
and log
ba.
page no 228 note ‡ Of special importance to subsequent developments (in the general mathematical theory) are the particular cases:
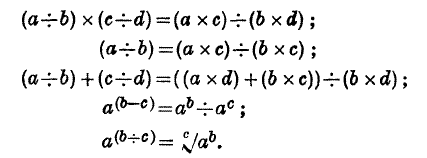
(All quite simple, for natural numbers a, b, ... .)
page no 228 note § Nothing is more interesting than the relation (especially in Mathematics) of proof to discovery. Note, for example, the propositions not true, which are of the same general type of those that are true; thus ab ≠ba and (a±b) c ≠ac ±bc .
page no 228 note ‖ See § 6, 3, infra.
page no 229 note * The discovery of this mode of notation was itself (as is well known) an age-long process; but, once discovered, it was the end of that particular search (see, however, the next footnote). Compare the Greek (alphabetical) mode of notation—as quite inadequate human invention; and the Roman—sound in principle, so far as it goes, but arithmetically inflexible, and ill-adapted to the infinity of the Natural Number sequence.
page no 229 note † See appended Note, on the Basic Radix.
page no 229 note ‡ The case of Angle is closely analogous. Practically all other measurement is secondary to these cases—in terms of axiomatic propositions of “Proportion”.
page no 229 note § A different use of the term “addition”, initially independent of its use in the Natural Number system—but correlated with that use, in the general theory of “Number” and “Ratio”.
page no 229 note ‖ Vide § 6, infra; in particular, § 6, 2, 2.
page no 229 note ** See § 1, 2, 2, with footnote.
page no 230 note * In this scheme of notation—the “product” n.OA being essentially non-commutative—only the number (n) is an admissible (consequent) “divisor”. There is no place for such a form as n/L—if L denotes a length—nor even for ON/OA (since, as ON/n = OA implies ON = n.OA, ON/OA = n would imply ON = OA.n); hence the logical importance of the special “ratio” form ON: OA.
The notation is, to some extent, conventional (inventional)—but, however expressed, the facts are plain; and they hold good for any such case as Y = n.X.—if X, Y denote quantities of any (the same) kind, other than “number”.
page no 230 note † The sequence—“in harmonic progression”—of all possible sub-units (say, U/2, U/3, ...) is not of practical significance; but such a sequence of sub-multiples is of fundamental theoretical importance in the general theory of “Number” and “Ratio”.
page no 231 note * The formal reduction of the number of these generalised “operations”, from seven to six—by the formal inclusion of “Evolution” in “Involution”—is one of the details highly significant of discovery.
A simple example of the (very restricted) type of Natural Number case, from which these generalisations originate, is (see §4,2):—Given ON
1 = 8.OA, ON
2 =2.OA, then (corresponding to the number-operations a ± b, 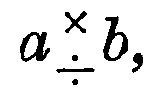 ab, log
ba), ON
3 = 10.OA, ON
4 = 6.OA, ON
5 = 16.OA, ON
6 = 4.OA, ON
7 = 64.OA, ON
8 = 3.OA—where the given numbers 8 and 2 have had to be very specially chosen. (If it were important to bring in
ab, log
ba), ON
3 = 10.OA, ON
4 = 6.OA, ON
5 = 16.OA, ON
6 = 4.OA, ON
7 = 64.OA, ON
8 = 3.OA—where the given numbers 8 and 2 have had to be very specially chosen. (If it were important to bring in ![]() , as well, we would have to take such given numbers as 64 and 2.)
, as well, we would have to take such given numbers as 64 and 2.)
page no 231 note † There is then a P 7 on that half-line—and there may be another on the opposite half-line (but this latter fact gets into true perspective in the context of § 6, 1, 2).
page no 231 note ‡ Again, one point P 8, then, on the half-line O→A→.
page no 231 note § It is, again, highly significant of discovery that the geometrical correlative of “number” is precisely “two-dimensional”, in this way: actually “(n-) dimensional” at all, and for that particular value of n (neither 1 nor 3, nor any other). The facts of Vector Analysis—for a 3-dimensional system of vectors, etc.—only add to the interest of the whole process of discovery.
page no 232 note * Vide § 1, 2, 1, supra.
page no 232 note † The “ratio” of any two vectors of the plane-system being, in fact, the “(complex) number”, of which the “modulus” is the “positive real number” which is the “ratio” of their lengths —and the “Amplitude”-angle (used through “the real numbers” which are (a) its measure and (b) trigonometric functions of it), the (corresponding) inclination of their directions. (This, of course, belongs to the detailed process to which § 6, 3 has reference.)
page no 232 note ‡ Vide § 2, with footnotes.
page no 232 note § The original intention was to include in the present paper an outline of this process; but that has proved impossible, within conceivable limits of such a paper. It will have to be done otherwise. The remarkable—characteristic, and quite astonishing—simplicities of the process need emphasizing.
page no 233 note * By E. W. Phillips in a paper on “Binary Calculations”, communicated to the Institute of Actuaries on 27th Jan. 1936. (The writer has seen only an “account” of the paper—in an Insurance journal.)