The Cissoid of Diocles

Extract

The construction, presumably used by Diocles, who flourished in the second century B.C., for the cissoid is as follows.

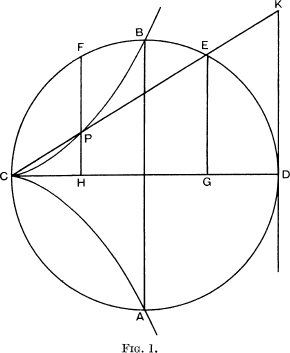
Let AB, CD be perpendicular diameters of a circle. Let E, F be points on the quadrants BD, BC such that the arcs BE, BF are equal. Draw EG, FH perpendicular to CD. Join CE and let P be the point of intersection of CE and FH The cissoid is the locus of P corresponding to points E, F on the quadrants BD, BC such that the arcs BE, BF are equal.