Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-11T22:10:36.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximations to n√1+x where n is an integer and 0<x<1

Published online by Cambridge University Press:  03 November 2016

J.M. Child
Get access Rights & Permissions [Opens in a new window]

Extract

If we seek approximations to 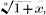in the form

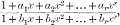
of such a nature that the fraction gives, on performing the division, an infinite series whose first 2r+1 terms are identical with the first 2r+1 terms of the Binomial Expansion for 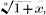we shall obtain 2r equations of the form

Type
Research Article
Information
The Mathematical Gazette , Volume 8 , Issue 124 , July 1916 , pp. 289 - 295
Copyright
Copyright © The Mathematical Association 1916

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 293 note * By the use of the caluculus for first even convergent.

page 295 note * Taking µ=•4342944819 from Chambers. For closer approximations µ would have to be calculated from the convergents above or closer ones.