Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-12-02T20:53:19.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximating Lipschitz and continuous functions by polynomials; Jackson’s theorem

Published online by Cambridge University Press:  03 July 2023

G. J. O. Jameson
G. J. O. Jameson*
Affiliation:
13 Sandown Road, Lancaster LA1 4LN e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The celebrated theorem of Weierstrass, dating from 1885, states that continuous functions can be uniformly approximated by polynomials on any bounded, closed interval. But just how well can we approximate by polynomials of a certain degree? Let us introduce some notation to facilitate the discussion. For an interval I (which will usually be 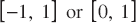), denote by C (I) the space of continuous functions on I, and write 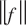for 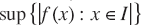(the notation 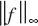is often used). Uniform convergence of fn to f (on I) equates to the statement that 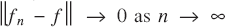. Denote by 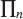the space of polynomials of degree not more than n. This is a linear subspace of C (I) of dimension n + 1. We write

Type
Articles
Information
The Mathematical Gazette , Volume 107 , Issue 569 , July 2023 , pp. 273 - 285
Check for updates
Copyright
© The Authors, 2023. Published by Cambridge University Press on behalf of The Mathematical Association

References

Jameson, G. J. O., How close is the approximation by Bernstein polynomials? Math. Gaz. 104 (November 2020) pp. 484–494.CrossRefGoogle Scholar
Jackson, D., On approximation by trigonometric sums and polynomials, Trans. Amer. Math. Soc. 13 (1912) pp. 491–515.CrossRefGoogle Scholar
Korovkin, P. P., Linear operators and approximation theory, Hindustan (1960).Google Scholar
Meinardus, G., Approximation of functions: theory and numerical methods, Springer (1967).Google Scholar
Rivlin, Theodore J., An introduction to the approximation of functions, Dover (1969).Google Scholar
Cheney, E. W., Introduction to approximation theory, McGraw Hill (1966).Google Scholar
Walker, P. L., The theory of fourier series and integrals, Wiley (1986).Google Scholar
Edwards, R. E., Fourier series: a modern introduction, vol. 1, Springer (1979).CrossRefGoogle Scholar