Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-30T18:55:58.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Tropical cycles

Published online by Cambridge University Press:  18 June 2020

S. Northshield
S. Northshield*
Affiliation:
SUNY, Plattsburgh, NY, USA, e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

The Lyness equation (1)

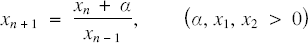\begin{equation}{X_{n + 1}} = \frac{{{X_n} + a}}{{{X_{n - 1}}}},\,(a,{x_1},{x_2} > 0)\end{equation}
was introduced in 1947 by Lyness [1] and it, and related equations, have long been studied; see [1, 2, 3, 4, 5, 6, 7] and references therein. Perhaps surprisingly, all solutions of (1) are bounded (i.e. for all x1, x2, the set {xn} is bounded) - we will show that below. Furhter, there often exist periodic solutions (i.e. xn = xn+N for all n in which case we say that (xn) has period N). See [8] for a discussion of which periods are possible for a given α. We note that a sequence of period, say, 5 also has periods 10, 15, 20, …. so we use the term minimal period for the smallest positive N such that xn = xn+N for all n.

Type
Articles
Information
The Mathematical Gazette , Volume 104 , Issue 560 , July 2020 , pp. 225 - 234
Check for updates
Copyright
© Mathematical Association 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Lyness, C., Cycles, Math. Gaz. 26 (February 1942) p. 62.CrossRefGoogle Scholar
Fomin, S., Cluster Algebras master class, videos of series of talks on cluster algebras, accessed May 2019 at http://qgm.au.dk/video/mc/cluster/Google Scholar
Gasull, A., Mañosa, V., Xarles, X., Rational periodic sequence for the Lyness recurrence, Cornell University (2012) available at arXiv.org.abs/1004.5511Google Scholar
Griffiths, J., Lyness Cycles, Elliptic Curves, and Hikorsky Triangles, accessed March 2019 at www.s253053503.websitehome.co.uk/jg-msc-uea/thesis-final-11-2-2012.pdfGoogle Scholar
Kocic, V. and Ladas, G., Global behavior of nonlinear difference equations of higher order with applications, Kluwer Academic Publishers, Norwell, MA (1993).CrossRefGoogle Scholar
Northshield, S., A Lyness equation for graphs, J. Difference Equ. Appl., 18(7) (2012) pp. 1183–1191.CrossRefGoogle Scholar
Zeeman, C., Geometric unfolding of a difference equation, (notes of a talk given May 19, 1997 at Cambridge Univ.), accessed March 2019 at zakuski.utsa.edu/˜gokhman/ecz/geometric unfolding.pdfGoogle Scholar
Bastien, G. and Rogalski, M., Global behavior of the solutions of Lyness' difference equation u n+2u n = u n+1 + a, J. Difference Equ. Appl. 10(11) (2004) pp. 997–1003.CrossRefGoogle Scholar
Barbeau, E., Gelbord, B., and Tanny, S., Periodicities of solutions of the generalized Lyness recursion, J. Difference Equ. Appl. 1(3) (1995) pp. 291–306.CrossRefGoogle Scholar
Dolan, S., Lyness cycles, Math. Gaz. 101 (July 2017), pp. 193–207.CrossRefGoogle Scholar
Speyer, D., Sturmfels, B., Tropical Mathematics, Math. Mag. 82(3) (2009) pp. 163–173.CrossRefGoogle Scholar