Article contents
A Proof of Cauchy’s Inequality and a New Generalization
Published online by Cambridge University Press: 03 November 2016
Extract
If a1, …, an and b1, …, bn are two sets of real numbers, then (a1b1 + … + anbb)2 ≤ (a12 + … + an2)(b12 + … + bn2), the equality holding if and only if either 3 a real number λ such that ar — λbr (r = 1, …, n) with some br ≠ 0 or b1 = … = bn = 0. Write a = (a1, …, an) and b = (b1, …, bn). Suppose a ≠ 0 and b ≠ 0, for otherwise the inequality is trivial. Write с = a — λb.
Choose λ so as to make b, c=0, i.e take 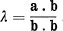
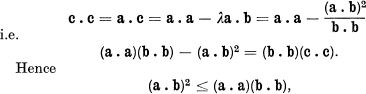
the equality holding if and only if e=0, i.e if and only if a=λb,
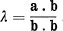
2. Suppose x1...,xn and y1 are two sets of linearly independent vectors in the space E defined on the previous note.
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 1963
- 2
- Cited by


