Article contents
Extract
I recently came across a very appealing result about the product of the lengths of the chords of a regular polygon with n sides inscribed in a unit circle. If one vertex is selected and the product of the chord lengths from that vertex to each of the others is evaluated, the result is just n. There is a simple proof. Consider such a polygon and denote its vertices by the points A0, A1, … , An. Suppose that O is the centre of the circle and the origin of the complex plane. The roots of the equation
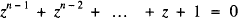
are just 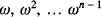 where ω is a primitive nth root of unity. Each of these roots represents one of the vertices. Suppose for convenience that the real number 1 is represented by A0.
where ω is a primitive nth root of unity. Each of these roots represents one of the vertices. Suppose for convenience that the real number 1 is represented by A0.
- Type
- Articles
- Information
- Copyright
- Copyright © Mathematical Association 2002
- 4
- Cited by


