No CrossRef data available.
Article contents
On the Intersections of a Central Conic and its Principal Hyperbolas
Published online by Cambridge University Press: 03 November 2016
Extract
Let an ellipse or a hyperbola be given by the equation
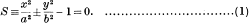
Then, following Vaidyanathaswamy [8, p. 124], we shall refer to a hyperbola H having its asymptotes parallel to the principal axes of S as a principal hyperbola of S. H is thus given by an equation of the type
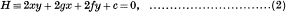
and it is uniquely determined when we know three of its intersections with S. It is one of the purposes of this article to bring together some of the elementary properties of H which have been ignored, quite unjustifiably, by most of the textbooks on conic sections produced after Casey's Analytical Geometry [2]. Another purpose which it is hoped the article will serve is that of bringing within easy reach of students, who have had only a preliminary course in geometries of two and three dimensions, some of Vaidyanathaswamy's investigations into the concurrency of normals to a central conic [6].
- Type
- Research Article
- Information
- Copyright
- Copyright © The Mathematical Association 1951


