Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-02T19:20:51.776Z Has data issue: false hasContentIssue false
  • English
  • Français

A new algorithm for computing the logarithmic function

Published online by Cambridge University Press:  01 August 2016

Stuart Simons  and
Andrew Tworkowski
Stuart Simons
Affiliation:
School of Mathematical Sciences, Queen Mary College, University of London, Mile End Road, London E1 4NS, e-mails: [email protected], [email protected]
Andrew Tworkowski
Affiliation:
School of Mathematical Sciences, Queen Mary College, University of London, Mile End Road, London E1 4NS, e-mails: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

The values of many functions, for example sinx or cosx, can be computed efficiently for arbitrary values of x from their known power series expansions. However, for the logarithmic function this is not so straightforward. There does not exist an expansion of ln x as a power series in x, the closest to it mathematically being an infinite power series in 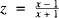of the form

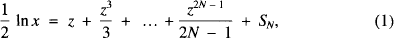
where 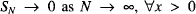(see [1]).

Type
Articles
Information
The Mathematical Gazette , Volume 89 , Issue 515 , July 2005 , pp. 212 - 221
Copyright
Copyright © The Mathematical Association 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abramowitz, M. and Stegun, I. A. Handbook of mathematical functions, Dover Publications (1965) p. 68.Google Scholar
2. Press, W. H. Flannery, B. P. Teukolsky, S. A. and Vetterling, W. T. Numerical recipes – the art of scientific computing, Cambridge University Press (1987).Google Scholar