Lamé Ovals

Extract

Generalization of the ellipse to

is credited to Gabriel Lamé, the 19th-century French physicist and the eponym of this family of curves. Lamé curves have recently been taken out of mathematical limbo due to their appeal to certain designers and architects. Particularly to be mentioned is Piet Hein, the contemporary Danish poet-designer-scientist (and inventor of mathematical games) who rediscovered the curves and has been using “superellipses” (Lamé curves with n > 2, and therefore oval) in objets d’art, furniture, pottery, fabric patterns, and so on. 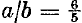His major achievement to date is a sunken oval shopping plaza, promenade, and pool in the centre of Stockholm; its shape is a superellipse with and 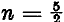. Derivatively, Gerald Robinson, a Toronto architect, has incorporated a superelliptic parking garage into a shopping complex (called a Superblock) in downtown Peterborough, Ontario; the parameters are 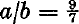and n = 2.71828 … (the exponential coefficient). In such urban contexts the two-parameter super-ellipse is efficiently tailorable to the dimensions of the site. It is said to be very elegant.