Article contents
Integral powers of order three Latin square matrices
Published online by Cambridge University Press: 01 August 2016
Extract
An order-n Latin square contains numbers, each of which is one of a set of n real numbers, 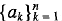 , arranged in the form of an n × n matrix, in such a way that each row and each column of the matrix contains all n numbers. Euler (1707-1783) was the first to study the properties of Latin squares and they have been the focus of continued attention since. Studies of Latin squares naturally lead one to elements of group theory and of matrix theory. As will be shown in this note, both of these features may offer interesting investigative opportunities for classroom discussions of the permutation group on three symbols and of the algebra of the associated permutation matrices.
, arranged in the form of an n × n matrix, in such a way that each row and each column of the matrix contains all n numbers. Euler (1707-1783) was the first to study the properties of Latin squares and they have been the focus of continued attention since. Studies of Latin squares naturally lead one to elements of group theory and of matrix theory. As will be shown in this note, both of these features may offer interesting investigative opportunities for classroom discussions of the permutation group on three symbols and of the algebra of the associated permutation matrices.
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 2009
References
- 1
- Cited by


