Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Al Rabee, Faeik T.
Al-Rimawi, Ashraf
and
Gitlin, Richard D.
2018.
Channel Capacity in a Dynamic Random Waypoint Mobility Model.
p.
711.
Mayer, Alexander
2019.
Estimation and Inference in Adaptive Learning Models with Slowly Decreasing Gains.
SSRN Electronic Journal,
Bai, Tong
Wang, Jingjing
Ren, Yong
and
Hanzo, Lajos
2019.
Energy-Efficient Computation Offloading for Secure UAV-Edge-Computing Systems.
IEEE Transactions on Vehicular Technology,
Vol. 68,
Issue. 6,
p.
6074.
Eggers, Patrick C. F.
Angjelichinoski, Marko
and
Popovski, Petar
2019.
Wireless Channel Modeling Perspectives for Ultra-Reliable Communications.
IEEE Transactions on Wireless Communications,
Vol. 18,
Issue. 4,
p.
2229.
Akkouchi, Mohamed
and
Ighachane, Mohamed Amine
2019.
Refinements of Some Recent Inequalities for Certain Special Functions.
Annales Mathematicae Silesianae,
Vol. 33,
Issue. 1,
p.
1.
Abolhassani, Bahman
Tadrous, John
and
Eryilmaz, Atilla
2019.
Wireless Multicasting for Content Distribution: Stability and Delay Gain Analysis.
p.
1.
Smetana, Kathrin
Zahm, Olivier
and
Patera, Anthony T.
2019.
Randomized Residual-Based Error Estimators for Parametrized Equations.
SIAM Journal on Scientific Computing,
Vol. 41,
Issue. 2,
p.
A900.
Atta, A. G.
Moatimid, G. M.
and
Youssri, Y. H.
2019.
Generalized Fibonacci Operational Collocation Approach for Fractional Initial Value Problems.
International Journal of Applied and Computational Mathematics,
Vol. 5,
Issue. 1,
Liu, Siqi
Melia, Adrian
Song, Xiaojing
and
Tippett, Mark
2020.
Singular diffusions, constant elasticity of variance processes and logarithmic rates of return.
The European Journal of Finance,
Vol. 26,
Issue. 9,
p.
837.
Mathias, Simon A.
Dentz, Marco
and
Liu, Qingquan
2020.
Gas Diffusion in Coal Powders is a Multi-rate Process.
Transport in Porous Media,
Vol. 131,
Issue. 3,
p.
1037.
Mahata, Shantiram
and
Sinha, Rajen Kumar
2020.
On the existence, uniqueness and stability results for time-fractional parabolic integrodifferential equations.
Journal of Integral Equations and Applications,
Vol. 32,
Issue. 4,
Beghin, Luisa
and
Gajda, Janusz
2020.
Tempered Relaxation Equation and Related Generalized Stable Processes.
Fractional Calculus and Applied Analysis,
Vol. 23,
Issue. 5,
p.
1248.
Tarable, Alberto
and
Escribano, Francisco J.
2020.
Chaos-Based Anytime-Reliable Coded Communications.
IEEE Systems Journal,
Vol. 14,
Issue. 2,
p.
2214.
Chavez, Gordon V.
2020.
Dynamic tail inference with log-Laplace volatility.
Extremes,
Vol. 23,
Issue. 2,
p.
287.
Kakavas-Papaniaros, P. A.
2020.
On the distribution of particles in propellant solids.
Acta Mechanica,
Vol. 231,
Issue. 3,
p.
863.
Bhardwaj, Pranay
and
Zafaruddin, S. M.
2021.
Performance of Dual-Hop Relaying for THz-RF Wireless Link Over Asymmetrical $\alpha$-$\mu$ Fading.
IEEE Transactions on Vehicular Technology,
Vol. 70,
Issue. 10,
p.
10031.
Linares Cedeño, Francisco X.
and
Nucamendi, Ulises
2021.
Revisiting cosmological diffusion models in Unimodular Gravity and the H0 tension.
Physics of the Dark Universe,
Vol. 32,
Issue. ,
p.
100807.
Bernardo, Neil Irwin
Zhu, Jingge
and
Evans, Jamie
2021.
On Minimizing Symbol Error Rate Over Fading Channels With Low-Resolution Quantization.
IEEE Transactions on Communications,
Vol. 69,
Issue. 11,
p.
7205.
Das, Pratibhamoy
and
Rana, Subrata
2021.
Theoretical prospects of fractional order weakly singular Volterra Integro differential equations and their approximations with convergence analysis.
Mathematical Methods in the Applied Sciences,
Vol. 44,
Issue. 11,
p.
9419.
Budde, Christian
2021.
Positive Desch-Schappacher perturbations of bi-continuous semigroups on AM-spaces.
Acta Scientiarum Mathematicarum,
Vol. 87,
Issue. 3-4,
p.
571.
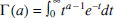 for a > 0. By splitting this integral at a point x ⩾ 0, we obtain the two incomplete gamma functions:
for a > 0. By splitting this integral at a point x ⩾ 0, we obtain the two incomplete gamma functions: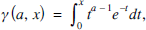 (1)
(1)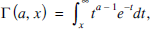 (2)
(2)

