Hostname: page-component-cc8bf7c57-pd9xq Total loading time: 0 Render date: 2024-12-11T22:56:08.974Z Has data issue: false hasContentIssue false
  • English
  • Français

Conics twinned with two special circles

Published online by Cambridge University Press:  23 January 2015

Christopher Bradley
Christopher Bradley*
Affiliation:
Flat 4, Terrill Court, 12-14 Apsley Road, Bristol BS8 2SP
Get access Rights & Permissions [Opens in a new window]

Extract

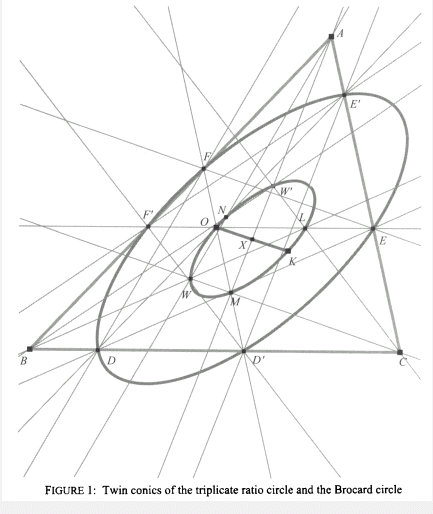
Throughout the article we use areal (or barycentric) coordinates. The side lengths of BC, CA, AB are denoted as usual by a, b, c and for brevity and ease of reading we write a2 = p, b2 = q, c2 = r. The symmedian point K then has coordinates (a2, b2, c2 ) replaced by (p, q, r), it being the isogonal conjugate of the centroid, and the circumcentre O then has coordinates (a2(b2 + c2 − a2), b2(c2 + a2 − b2), c2(a2 + b2 − c2)) replaced by (p(q + r − p), q(r + p − q), r(p + q − r)). The construction of the triplicate ratio circle (also known as the Lemoine circle) and the Brocard circle is replicated but starting with the circumcentre O rather than the symmedian point K. It is found that the triplicate ratio circle is then replaced by a conic cutting internally each side of ABC twice and having centre X the midpoint of OK. The Brocard circle is replaced by a conic passing through O and K and also having centre X the midpoint of OK. These we define as the twin conics.

Type
Articles
Information
The Mathematical Gazette , Volume 96 , Issue 536 , July 2012 , pp. 236 - 242
Copyright
Copyright © The Mathematical Association 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bradley, C. J., The algebra of geometry, Highperception (2007).Google Scholar
2. Johnson, R. A., Advanced Euclidean geometry, Now available in Dover Books in mathematics, originally published in 1924.Google Scholar
3. Honsberger, R., Episodes in nineteenth and twentieth century Euclidean geometry, The Mathematical Association of America (1995).Google Scholar