Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-12T00:59:15.241Z Has data issue: false hasContentIssue false
  • English
  • Français

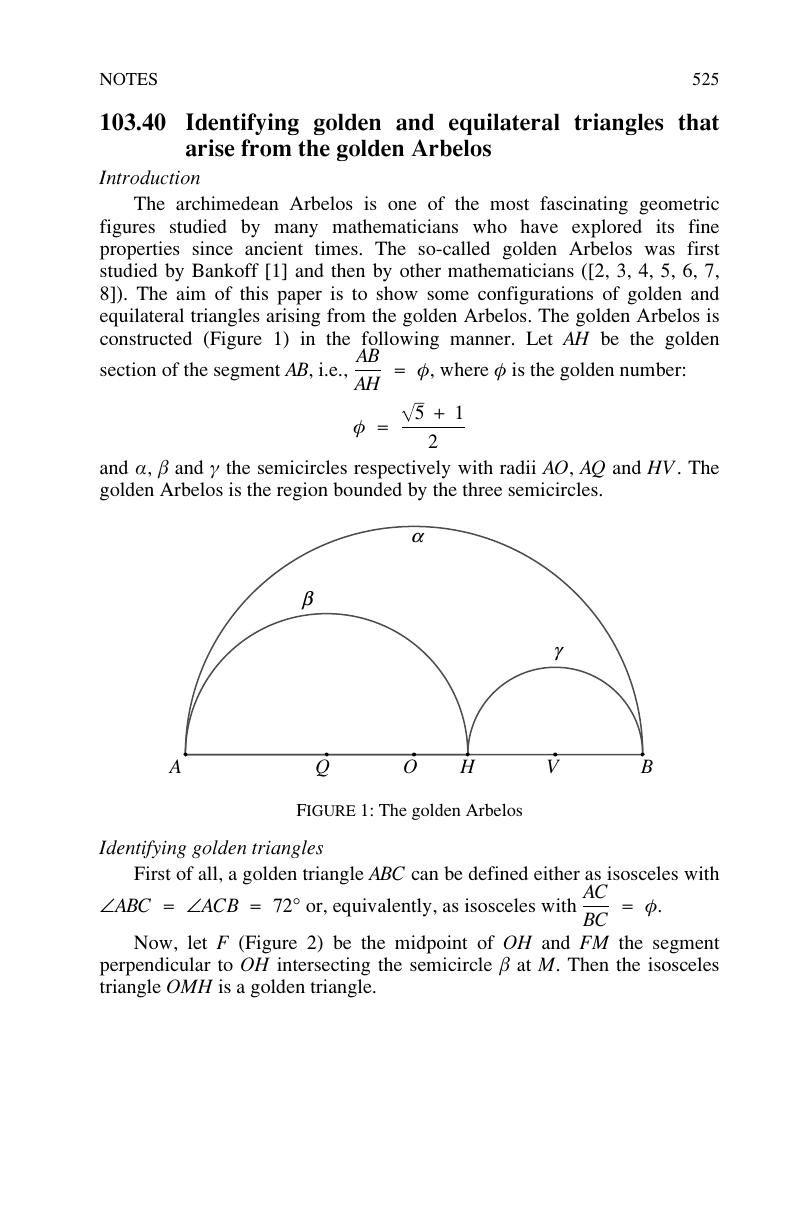
103.40 Identifying golden and equilateral triangles that arise from the golden Arbelos

Published online by Cambridge University Press:  21 October 2019

Aldo Scimone
Aldo Scimone*
Affiliation:
Via Costantino Nigra 30, 90141 Palermo. Sicily e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An abstract is not available for this content so a preview has been provided. Please use the Get access link above for information on how to access this content.
Image of the first page of this content. For PDF version, please use the ‘Save PDF’ preceeding this image.'
Type
Notes
Information
The Mathematical Gazette , Volume 103 , Issue 558 , November 2019 , pp. 525 - 531
Copyright
© Mathematical Association 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bankoff, L., The golden arbelos, Scripta Mathematica 21 (1955) pp. 70–76.Google Scholar
Bankoff, L., The marvelous Arbelos, The lighter side of mathematics (Guy, R. K., Woodrow, R. E., eds.) The Mathematical Association of America, Washington, DC (1994) pp. 247–253.Google Scholar
Okumura, H., A note on regular pentagons arising from the golden arbelos, Glob. J. Adv. Class. Mod. Geom. 5 (2016) pp. 75–77.Google Scholar
Okumura, H., Watanabe, M., The arbelos: a cosmos made by three semicircles, Iwanami Shoten (in Japanese) (2010).Google Scholar
Gardner, M., Mathematical games: The diverse pleasures of circles that are tangent to one another, Sci. Amer. 240 (1979) pp. 18–28; reprinted in Fractal music, hypercards and more, W. H. Freeman (1992) pp. 149-166.CrossRefGoogle Scholar
Stakhov, A., Olsen, S., The mathematics of harmony: from Euclid to contemporary mathematics and computer science, World Sci. (2009).CrossRefGoogle Scholar
Dodge, C. W., Schoch, T., Woo, P. Y., Yiu, P., Those ubiquitous Archimedean circles, Math. Mag. 72 (1999) pp. 202–213.CrossRefGoogle Scholar
Scimone, A., Some nice relations between right-angled triangles and the Golden Section, Teaching Mathematics and Its Applications, (2011) pp. 85–94.Google Scholar