1. Introduction
Does credit matter in recent economic analysis? The credit sector has become widely viewed as one of the most important driving forces of economic fluctuation. The credit sector and credit-related variables have recently been found to be both causative factors in the occurrence of economic events and one of the variables most affected by the consequences of economic events. For example, the prevailing view of the Great Recession is that the failure in credit management was associated with the financial crisis. More recently, an unusual surge in credit supply occurred during the COVID-19 pandemic outbreak.
According to the Federal Reserve Board Payment Study (2019), the number of credit card payments and the amount of those credit card payments, both general purpose and private label, are increasing rapidly.Footnote 1 The number of credit card payments and the amount of credit card payments were 26.8 billion and $2.55 trillion in 2012, 33.7 billion and $3.05 trillion in 2015, and 44.7 billion and $3.98 trillion in 2018, respectively. The annual growth rate of the number of credit card payments and the amount of credit card payments were 7.9% and 6.2% from 2012 to 2015 and 9.9% and 9.3% from 2015 to 2018, respectively. According to the St. Louis Federal Reserve Bank’s FRED database, the value of outstanding credit card debt in the US has recently surpassed 1 trillion dollars. The increasing credit utilization has resulted in increasing research on its role in the economy, expanding rapidly since 2016 on early research beginning with Brito and Hartley (Reference Brito and Hartley1995).
But the conventional monetary aggregates do not include the deferred payment transaction services of credit cards. We hypothesize that the credit-card-augmented Divisia monetary aggregates (hereafter “credit-augmented Divisia”), introduced by Barnett and Su (Reference Barnett and Su2016, Reference Barnett and Su2018) and Barnett et al. (Reference Barnett, Chauvet, Leiva-Leon and Su2023), would have more explanatory power than the traditional monetary aggregates, both empirically and theoretically. Simple sum monetary aggregates cannot include credit card services, since credit card balances are liabilities while monetary balances are assets, and accounting conventions do not permit adding liabilities to assets. But Divisia aggregation is based on economic aggregation theory and index number theory, which aggregate over service flows, regardless of whether produced from assets or liabilities.
In fact, in a New Keynesian framework with imperfect markets, we find theoretical reason to doubt the existence of an aggregator function over monetary services without credit card deferred payment services included. Without perfect markets, we find the need for an interaction between monetary services and credit card deferred payment services in utility functions. That interaction would violate the blockwise weak separability condition needed to exclude credit card services from a monetary services aggregator function.
Existing empirical research using credit-augmented Divisia includes Barnett and Su (Reference Barnett and Su2016, Reference Barnett and Su2018), Barnett and Liu (Reference Barnett and Liu2019), Barnett and Park (Reference Barnett and Park2024), Barnett and Park (Reference Barnett and Park2023), Liu and Serletis (Reference Liu and Serletis2020, Reference Liu and Serletis2023), and Liu et al. (Reference Liu, Dery and Serletis2020). We continue in that new tradition with further empirical and theoretical evidence using the aggregation-theoretic credit-augmented Divisia, available from the Center for Financial Stability (CFS) in NY City. There also is an even newer credit-card-augmented Divisia monetary aggregate that is Gross Domestic Product (GDP) optimized using nowcasting methodology. That newer credit-augmented Divisia aggregate was first introduced by Barnett et al. (Reference Barnett, Chauvet, Leiva-Leon and Su2023), but those data are not yet available to the public from the CFS and therefore are not used in our current study.
We use two approaches to investigate the usefulness of the credit-augmented Divisia. First, we expand upon the New Keynesian DSGE framework to include economic agent behavior in the credit sector. We do so including three different monetary aggregates: (1) the Constant Elasticity of Substitution (CES) aggregator function, defining the microeconomic theoretic (true) monetary aggregate, (2) the credit-card-augmented Divisia monetary aggregate, and (3) the simple sum monetary aggregate. By comparing the behavior of impulse responses to various shocks imposed on two differently defined monetary aggregates, credit-augmented Divisia versus simple sum, we determine which behaves most similarly to the shocked theoretical aggregator function. Since the macroeconomic model does not have classical structure with economic agents being price takers in perfect markets, the known approximation properties of the Divisia index in neoclassical microeconomic theory cannot assure us of the results of this analysis in advance. We do not consider the usual Divisia monetary aggregate not containing credit card services, since one of our needed New Keynesian assumptions (equation 18) violates the weak separability condition for existence of a monetary aggregator function not including credit card services.
Second, we compare the empirical implications of credit-augmented Divisia before and after the Great Recession. At the zero-lower bound (ZLB), the federal funds rate provides an inappropriate monetary policy tool. Following the econometric approach in Christiano et al. (Reference Christiano, Eichenbaum and Evans1999) and Keating et al. (Reference Keating, Kelly, Smith and Valcarcel2019), we investigate whether credit-augmented Divisia can provide a more informative role as a monetary policy indicator than the traditional federal funds rate. We use two different data sets, each containing the federal funds rate and the credit-augmented Divisia M2 monetary aggregate as candidates for monetary policy indicators. By using recursive VAR, we track the impulse responses with the two data sets to monetary policy shocks. We determine which candidate is consistent with the economic mechanism. We thereby determine which one, federal funds rate or credit-augmented Divisia, can serve as the most informative policy indicator.
As Bernanke and Blinder (Reference Bernanke and Blinder1988) emphasized, the critical view of the dichotomy between money and credit was reconfirmed by Liu et al. (Reference Liu, Dery and Serletis2020), who criticize the New Keynesian model for ignoring the importance of the deferred payment liquidity services provided by credit card transactions. Pesaran and Xu (Reference Pesaran and Xu2016) track the impulse responses to credit (supply) shocks in a business cycle model. They consider the effect of banking sector credit shocks on the probability of default of the firm. A positive credit shock, defined as an increase in the loan to deposit ratio, increases output, consumption, hours of work, and productivity. The paper’s results emphasize the importance of credit in the New Keynesian model. Barnett and Park (Reference Barnett and Park2023) found that including the credit sector within a New Keynesian model reveals a greater cost of inflation than implied by the model without credit.
Since credit-augmented Divisia were introduced, many empirical applications and theoretical extensions have appeared. The results share the conclusion that credit-augmented Divisia track the theoretically exact liquidity services better than the alternatives and perform better than the alternatives for forecasting economic activity. For example, by using the multivariate state-space model, Barnett et al. (Reference Barnett, Chauvet and Leiva-Leon2016, Reference Barnett, Chauvet, Leiva-Leon and Su2023) found that nowcasting with the traditional Divisia monetary aggregates produces smaller mean square forecasting error than with the simple sum monetary aggregates, while nowcasting with the new credit-augmented Divisia aggregates yields a substantially smaller mean squared error than with the unaugmented original Divisia monetary aggregates. Dery and Serletis (Reference Dery and Serletis2019) have shown that the inference ability of the Divisia monetary aggregates is strongest when used with the broadest Divisia monetary aggregates. Liu and Serletis (Reference Liu and Serletis2020) investigate the cyclical properties of credit-augmented Divisia using Hamilton’s filter and Granger causality tests. They showed that both the narrow and broad credit-augmented Divisia monetary aggregates are superior to the traditional Divisia monetary aggregates. Performance in forecasting GDP using credit-augmented Divisia is clearly better than using the simple sum or the original unaugmented Divisia monetary aggregate.
Bayesian analysis reflecting economic beliefs also confirms the better performance of the credit-augmented Divisia monetary aggregates. By using sign-restricted VAR, Barnett and Park (Reference Barnett and Park2024) find a strong co-movement between the cumulative effect of credit supply shocks measured by lending rates and the historical behavior of the credit-augmented Divisia.
The structure of this paper is as follows: Section 2 discusses the DSGE New Keynesian framework including monetary aggregation. Section 3 investigates the model empirically using recursive VAR. We conclude in Section 4.
2. DSGE New Keynesian framework
We use an extension of the traditional New Keynesian framework to include a credit sector as a liquidity service provider consistent with microeconomic foundations. Throughout Section 2, we extend Belongia and Ireland’s (Reference Belongia and Ireland2014) New Keynesian DSGE structure, which supports use of the original Divisia monetary aggregates as true money. We do so using the structure in Barnett and Park (Reference Barnett and Park2023) as the benchmark model, except for the utility function and the monetary policy equations. The household’s and the bank’s behavior are changed substantially. The representative household can choose three options for liquidity service provision: the household can pay with cash, interest-bearing deposit, or credit card deferred payment transaction services. The bank is the sole financial intermediary and owns the credit cards sector.
For the credit sector, we make three assumptions. First, in accordance with Barnett and Su (Reference Barnett and Su2016, Reference Barnett and Su2018) and Barnett et al. (Reference Barnett, Chauvet, Leiva-Leon and Su2023), we do not include rotating balances used for transactions in prior periods as transaction services in the current period to avoid double counting of transaction services. Second, we assume the use of credit by the representative household always requires interest payment at rate
![]() $r_{t}^{CC}$
with “no grace period” (Brito and Hartley (Reference Brito and Hartley1995)). Since the model is of a representative household aggregated over all households, the assumption does not rule out the possibility that some credit users do not pay interest, such as credit card holders who always pay before the end of the month. Finally, debit cards, store cards, reward programs, and cashback programs will be ignored, since they are not consistent with some of our assumptions. Inclusion of rotating balances in the model would have no effect, since we do not include them in our definition of credit card deferred payment services. See, for example, Barnett and Su (Reference Barnett and Su2016, Reference Barnett and Su2018) and Barnett et al. (Reference Barnett, Chauvet, Leiva-Leon and Su2023).
$r_{t}^{CC}$
with “no grace period” (Brito and Hartley (Reference Brito and Hartley1995)). Since the model is of a representative household aggregated over all households, the assumption does not rule out the possibility that some credit users do not pay interest, such as credit card holders who always pay before the end of the month. Finally, debit cards, store cards, reward programs, and cashback programs will be ignored, since they are not consistent with some of our assumptions. Inclusion of rotating balances in the model would have no effect, since we do not include them in our definition of credit card deferred payment services. See, for example, Barnett and Su (Reference Barnett and Su2016, Reference Barnett and Su2018) and Barnett et al. (Reference Barnett, Chauvet, Leiva-Leon and Su2023).
Meanwhile, the key characterizations of the usual New Keynesian framework remain valid. Money is included in the utility function in accordance with a shopping time model (Goodfriend and McCallum (Reference Goodfriend and McCallum1988)) in which shopping time for consumption goods is a disutility. The intermediate goods-producing firms are monopolistically competitive with the quadratic cost of price adjustment (Rotemberg (Reference Rotemberg1982)).
2.1. Modeling
2.1.1. The representative household
The infinitely lived representative household’s utility function follows the shopping time model:
where
![]() $C_{t}$
is consumption,
$C_{t}$
is consumption,
![]() $\eta$
is the weight on leisure relative to consumption,
$\eta$
is the weight on leisure relative to consumption,
![]() $h_{t}$
is labor, and
$h_{t}$
is labor, and
![]() $h_{t}^{s}$
is shopping time for consumption goods, defined as:
$h_{t}^{s}$
is shopping time for consumption goods, defined as:
where
![]() $\chi$
manages the rate at which increased effort is needed to purchase goods and services as the household save money asset holdings.
$\chi$
manages the rate at which increased effort is needed to purchase goods and services as the household save money asset holdings.
![]() $v_{t}$
is the money demand shock, following an AR(1) process:
$v_{t}$
is the money demand shock, following an AR(1) process:
Here
![]() $v\gt 0$
is the steady-state level of real monetary services demanded relative to consumption, and
$v\gt 0$
is the steady-state level of real monetary services demanded relative to consumption, and
![]() $0\leq \rho _{v}\lt 1$
is a persistence parameter subject to calibration.
$0\leq \rho _{v}\lt 1$
is a persistence parameter subject to calibration.
During each period, the representative household has
![]() $M_{t-1}$
units of currency, carried over from the previous period,
$M_{t-1}$
units of currency, carried over from the previous period,
![]() $B_{t-1}$
units of bonds, and
$B_{t-1}$
units of bonds, and
![]() $s_{t-1}(i)$
ownership shares of each intermediate goods-producing firm,
$s_{t-1}(i)$
ownership shares of each intermediate goods-producing firm,
![]() $i\in [0,1]$
. At the beginning of each period, the household receives
$i\in [0,1]$
. At the beginning of each period, the household receives
![]() $Tr_{t}$
lump-sum transfer units from the government. The household has
$Tr_{t}$
lump-sum transfer units from the government. The household has
![]() $B_{t-1}$
units of bonds and buys
$B_{t-1}$
units of bonds and buys
![]() $B_{t}$
units of new bonds at the price of
$B_{t}$
units of new bonds at the price of
![]() $1/r_{t}$
dollars per bond, where
$1/r_{t}$
dollars per bond, where
![]() $r_{t}$
represents the gross nominal interest rate between the period
$r_{t}$
represents the gross nominal interest rate between the period
![]() $t$
and
$t$
and
![]() $t+1$
, and
$t+1$
, and
![]() $s_{t}(i)$
shares in each intermediate goods-producing firm,
$s_{t}(i)$
shares in each intermediate goods-producing firm,
![]() $i\in [0,1]$
, at the price of
$i\in [0,1]$
, at the price of
![]() $Q_{t}(i)$
dollars per share. The household holds
$Q_{t}(i)$
dollars per share. The household holds
![]() $N_{t}$
dollars of currency and borrows
$N_{t}$
dollars of currency and borrows
![]() $L_{t}$
dollars from the bank. The household utilizes credit card transaction services,
$L_{t}$
dollars from the bank. The household utilizes credit card transaction services,
![]() $CC_{t}$
, in dollars from the bank. The total nominal value of its deposits is
$CC_{t}$
, in dollars from the bank. The total nominal value of its deposits is
At the end of the period, the household owes the bank
![]() $r_{t}^{L}L_{t}$
and
$r_{t}^{L}L_{t}$
and
![]() $r_{t}^{CC}CC_{t}$
, where
$r_{t}^{CC}CC_{t}$
, where
![]() $r_{t}^{L}$
and
$r_{t}^{L}$
and
![]() $r_{t}^{CC}$
represent the gross nominal interest rate on loans and credit cards transaction services, respectively. That is, we assume the interest on credit card usage always accompanies every transaction service provided by credit cards (i.e., no grace period). The bank owes the household
$r_{t}^{CC}$
represent the gross nominal interest rate on loans and credit cards transaction services, respectively. That is, we assume the interest on credit card usage always accompanies every transaction service provided by credit cards (i.e., no grace period). The bank owes the household
![]() $r_{t}^{D}D_{t}$
dollars, where
$r_{t}^{D}D_{t}$
dollars, where
![]() $r_{t}^{D}$
represents the gross nominal interest rate on deposits. The household receives a nominal dividend payment of
$r_{t}^{D}$
represents the gross nominal interest rate on deposits. The household receives a nominal dividend payment of
![]() $F_{t}(i)$
for each share that it owns of each intermediate goods-producing firm. Finally, the household carries
$F_{t}(i)$
for each share that it owns of each intermediate goods-producing firm. Finally, the household carries
![]() $M_{t}$
units of currency into the next period, defined as:
$M_{t}$
units of currency into the next period, defined as:
.
The representative household’s maximization problem is
subject to the constraints (4) and (5), where
![]() $0\lt \beta \lt 1$
and
$0\lt \beta \lt 1$
and
![]() $\eta \gt 0$
, and where
$\eta \gt 0$
, and where
![]() $a_{t}$
is a preference shock following the AR(1) process:
$a_{t}$
is a preference shock following the AR(1) process:
where
![]() $0\leq \rho _{a}\lt 1$
.
$0\leq \rho _{a}\lt 1$
.
We define
![]() $M_{t}^{A}$
as a true aggregate of monetary services provided from currency
$M_{t}^{A}$
as a true aggregate of monetary services provided from currency
![]() $N_{t}$
, deposits
$N_{t}$
, deposits
![]() $D_{t}$
, and credit cards transactions
$D_{t}$
, and credit cards transactions
![]() $CC_{t}$
, according to
$CC_{t}$
, according to
which is in CES form. Following Lucas’s (Reference Lucas2000) argument, the true monetary aggregate has the CES specification for its aggregator function, since CES makes the model consistent with balanced growth. The parameters
![]() $\nu$
and
$\nu$
and
![]() $\xi$
stand for the steady-state ratio of currency and deposits to the total amount of monetary services, respectively. The parameter
$\xi$
stand for the steady-state ratio of currency and deposits to the total amount of monetary services, respectively. The parameter
![]() $\omega$
determines the elasticity of substitution among the monetary service components. Appendix A.1 explains the optimization problem for the representative household.
$\omega$
determines the elasticity of substitution among the monetary service components. Appendix A.1 explains the optimization problem for the representative household.
2.1.2. The representative final goods-producing firm
The final goods market is competitive, and during each period t the firm utilizes
![]() $Y_{t}(i)$
units of each intermediate good,
$Y_{t}(i)$
units of each intermediate good,
![]() $i\in [0,1]$
, to produce final goods quantity
$i\in [0,1]$
, to produce final goods quantity
![]() $Y_{t}$
. The production function for final goods is assumed to be
$Y_{t}$
. The production function for final goods is assumed to be
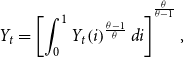 \begin{equation} Y_{t}=\left[\int _{0}^{1}Y_{t}\!\left(i\right)^{\frac{\theta -1}{\theta }}di\right]^{{^{\frac{\theta }{\theta -1}}}}, \end{equation}
\begin{equation} Y_{t}=\left[\int _{0}^{1}Y_{t}\!\left(i\right)^{\frac{\theta -1}{\theta }}di\right]^{{^{\frac{\theta }{\theta -1}}}}, \end{equation}
where
![]() $\theta \gt 1$
represents the elasticity of substitution between the various intermediate goods in producing the final good. The firm’s profit maximization problem is given by:
$\theta \gt 1$
represents the elasticity of substitution between the various intermediate goods in producing the final good. The firm’s profit maximization problem is given by:
for all
![]() $t=0,1,2,\ldots$
. The first-order conditions for this decision are
$t=0,1,2,\ldots$
. The first-order conditions for this decision are
for all
![]() $i\in [0,1]$
and
$i\in [0,1]$
and
![]() $t=0,1,2,\ldots$
. Since the final goods market is competitive, the final goods-producing firm earns zero profit. As a result, it follows that
$t=0,1,2,\ldots$
. Since the final goods market is competitive, the final goods-producing firm earns zero profit. As a result, it follows that
 \begin{equation} P_{t}=\left[\int _{0}^{1}P_{t}\!\left(i\right)^{1-\theta }di\right]^{\frac{1}{1-\theta }}, \end{equation}
\begin{equation} P_{t}=\left[\int _{0}^{1}P_{t}\!\left(i\right)^{1-\theta }di\right]^{\frac{1}{1-\theta }}, \end{equation}
in equilibrium for all
![]() $t=0,1,2,\ldots$
.
$t=0,1,2,\ldots$
.
2.1.3. The representative intermediate goods-producing firm
At each period t, the representative intermediate goods-producing firm utilizes
![]() $h_{t}(i)$
units of labor from the representative household to produce
$h_{t}(i)$
units of labor from the representative household to produce
![]() $Y_{t}(i)$
units of intermediate good
$Y_{t}(i)$
units of intermediate good
![]() $i$
with the CRS technology:
$i$
with the CRS technology:
where
![]() $Z_{t}$
represents the aggregate technology shock, assumed to follow a random walk with positive drift:
$Z_{t}$
represents the aggregate technology shock, assumed to follow a random walk with positive drift:
where
![]() $z\gt 1$
.
$z\gt 1$
.
In the New Keynesian framework, the intermediate goods-producing firms face monopolistic competition. At each period, the intermediate goods-producing firm sets the nominal price for its output, subject to the requirement that it satisfies the representative finished goods-producing firm’s demand. Following Rotemberg (Reference Rotemberg1982), the intermediate goods-producing firm is subject to a quadratic cost of adjusting its nominal price, measured in units of the finished good, and given by:
where
![]() $\phi \geq 0$
represents the magnitude of the price adjustment costs, and
$\phi \geq 0$
represents the magnitude of the price adjustment costs, and
![]() $\pi \gt 1$
represents the gross, steady-state inflation rate. Appendix A.2 explains the optimization problem for the intermediate goods-producing firm. To maximize real market value, the firm chooses the sequence for
$\pi \gt 1$
represents the gross, steady-state inflation rate. Appendix A.2 explains the optimization problem for the intermediate goods-producing firm. To maximize real market value, the firm chooses the sequence for
![]() $P_{t}(i)$
for all
$P_{t}(i)$
for all
![]() $t=0,1,2,\ldots$
.
$t=0,1,2,\ldots$
.
2.1.4. The representative bank’s credit sector
We assume the banking sector owns a credit cards business (Schuh et al. (Reference Schuh, Shy and Stavins2010)). The profit structure of the credit management business consists of (1) fees, such as penalty fees, annual fees, cash advance fees, and interchange fees, (2) interest, and (3) transaction fees from the business. As mentioned above, we focus only on the interest imposed on every credit card transaction for the aggregated representative household. Commercial bank interest payments on credit cards can be found in the St. Louis Federal Reserve’s database, FRED.
During each period, the representative bank receives
![]() $D_{t}$
dollars of deposits from the representative household, makes
$D_{t}$
dollars of deposits from the representative household, makes
![]() $L_{t}$
dollars of loans, and approves
$L_{t}$
dollars of loans, and approves
![]() $CC_{t}$
dollars of credit card transaction volumes from the representative household.Footnote 2 At the end of the period, the household receives interest on deposits,
$CC_{t}$
dollars of credit card transaction volumes from the representative household.Footnote 2 At the end of the period, the household receives interest on deposits,
![]() $r_{t}^{D}$
, pays interest on loans,
$r_{t}^{D}$
, pays interest on loans,
![]() $r_{t}^{L}$
, and pays interest on credit card transaction service,
$r_{t}^{L}$
, and pays interest on credit card transaction service,
![]() $r_{t}^{CC}$
. All interest rates are defined as gross rates.
$r_{t}^{CC}$
. All interest rates are defined as gross rates.
Let
![]() $\tau _{t}$
defines the bank’s reserve ratio, assumed to follows the AR(1) process:
$\tau _{t}$
defines the bank’s reserve ratio, assumed to follows the AR(1) process:
where
![]() $0\lt \tau \lt 1, 0\leq \rho _{\tau }\lt 1$
.
$0\lt \tau \lt 1, 0\leq \rho _{\tau }\lt 1$
.
The relationship between deposits and loans are determined by the bank’s chosen reserves ratio
![]() $\tau _{t}$
in accordance with the equation:
$\tau _{t}$
in accordance with the equation:
We assume the amount of monetary service provided by credit cards transactions is constrained by the aggregate amount of deposits in accordance with the equation:
where
![]() $\varpi _{t}$
refers to a shock on credit usage behavior. We assume that the credit:deposit ratio shock follows the AR(1) process:
$\varpi _{t}$
refers to a shock on credit usage behavior. We assume that the credit:deposit ratio shock follows the AR(1) process:
where
![]() $0\lt \varpi \lt 1, 0\leq \rho _{\varpi }\lt 1$
.
$0\lt \varpi \lt 1, 0\leq \rho _{\varpi }\lt 1$
.
We shall assume that constraint (18) will always be binding. After substitution into (8), a constraint connecting credit card volumes to deposits can violate the existence condition for a monetary aggregator function excluding credit card services, since monetary services may no longer be weakly separable from credit card services. We provide a clear example in equation (18a) below. Also such constraints imply the existence of a New Keynesian market imperfection in the market for credit card services. The rationale for constraint (18) or for more general constraints, such as (18a) below, could be viewed as supply side, since the source of funds for bank lending, including credit card lending, are primarily bank deposits. Nevertheless, consumers are assumed to take that bank constraint into consideration in their own consumer preferences.Footnote 3
The existence of separate aggregator functions for monetary assets and for credit card deferred payment services requires monetary assets and credit card deferred payment services to be in separate weakly separable blocks in the representative household’s utility function. That would be true if two conditions were met: (a) the marginal rate of substitution between currency and deposits must be independent of credit card deferred payment services, and (b) the marginal rate of substitution among the transaction services of different credit cards must be independent of currency and deposit quantities. Imposition of a constraint linking deposits to credit card deferred payment transaction services can violate condition (a) for existence of an aggregator function over monetary assets with credit card deferred payment services omitted from the aggregator function.Footnote 4
Equation (18) is a particularly simple way to connect deposits with credit card services. We chose that equation to simplify our empirical work. But the implications for separability of a connection between demand deposits and credit card services becomes especially clear with more general equations connecting deposits with credit card services. Consider, for example, the following habit formation version of equation (18):
where k is a constant and
![]() $CC_{t}-kCC_{t-1}$
is “supernumerary” consumption of credit card services in excess of habit formed quantities,
$CC_{t}-kCC_{t-1}$
is “supernumerary” consumption of credit card services in excess of habit formed quantities,
![]() $kCC_{t-1}$
, of those services. Equation (18a) can be solved for
$kCC_{t-1}$
, of those services. Equation (18a) can be solved for
![]() $CC_{t}$
and substituted into equation (8). Then it becomes clear that an aggregator function containing currency and demand deposits and not lagged credit card services does not exist. Factorability of a monetary aggregator function without credit card services does not exist. The weak separability condition for existence of a monetary aggregator function without credit card services is violated.
$CC_{t}$
and substituted into equation (8). Then it becomes clear that an aggregator function containing currency and demand deposits and not lagged credit card services does not exist. Factorability of a monetary aggregator function without credit card services does not exist. The weak separability condition for existence of a monetary aggregator function without credit card services is violated.
The reason for introducing equation (18) or more sophisticated versions, such as equation (18a), is interesting, perhaps surprising, and potentially important. Prior work on introducing credit card deferred payment services into Divisia monetary aggregates, including the seminal papers by Barnett and Su (Reference Barnett and Su2016, Reference Barnett and Su2018) and Barnett et al. (Reference Barnett, Chauvet, Leiva-Leon and Su2023), assumed perfect markets in a classical model. With complete decentralization to perfect markets, equations such as (18) or (18a) are not needed to complete the model. But without perfect markets in our current New Keynesian model, we found that there are not enough equations to solve the model without the introduction of a nonseparable interaction between credit card services and deposits. As a result, there is a very strong theoretical reason to include credit card services within Divisia monetary aggregates in New Keynesian models. Within the representative household’s utility function, the existence condition for a monetary services aggregator function can fail without inclusion of credit card services within the weakly separable block containing monetary services.Footnote 5
Following Belongia and Ireland (Reference Belongia and Ireland2014), the bank creates deposits with total real value
![]() $D_{t}/P_{t}$
at each period. Under the bank’s constant returns to scale (CRS) technology,
$D_{t}/P_{t}$
at each period. Under the bank’s constant returns to scale (CRS) technology,
![]() $x_{t}(D_{t}/P_{t})$
units of the finished goods are demanded. The bank’s credit card transaction services production are also consistent with this cost structure. The bank creates a credit cards account with total real value
$x_{t}(D_{t}/P_{t})$
units of the finished goods are demanded. The bank’s credit card transaction services production are also consistent with this cost structure. The bank creates a credit cards account with total real value
![]() $CC_{t}/P_{t}$
, and requiring
$CC_{t}/P_{t}$
, and requiring
![]() $x_{t}(CC_{t}/P_{t})$
units of finished goods. We assume the bank earns profits from the interest on credit card transaction volumes. We assume the existence of a financial sector cost shock,
$x_{t}(CC_{t}/P_{t})$
units of finished goods. We assume the bank earns profits from the interest on credit card transaction volumes. We assume the existence of a financial sector cost shock,
![]() $x_{t}$
, following the AR(1) process:
$x_{t}$
, following the AR(1) process:
where
![]() $x\gt 0$
and
$x\gt 0$
and
![]() $0\leq \rho _{x}\lt 1$
.
$0\leq \rho _{x}\lt 1$
.
The bank’s nominal profits during the period
![]() $t$
are
$t$
are
Substituting (17) and (18) into (21), we acquire the optimization problem with respect to
![]() $D_{t}$
. Finally, we obtain the equation that explains the relationship among the interest rates:
$D_{t}$
. Finally, we obtain the equation that explains the relationship among the interest rates:
This relationship holds in equilibrium at each period.
2.1.5. Efficient allocations and output gap
We consider a central bank using a modified Taylor rule. A social planner allocates
![]() $h^{*}(i)$
units of the representative household’s labor to produce
$h^{*}(i)$
units of the representative household’s labor to produce
![]() $Y_{t}^{*}(i)$
units of intermediate good
$Y_{t}^{*}(i)$
units of intermediate good
![]() $i\in [0,1]$
, while using those intermediate goods to produce
$i\in [0,1]$
, while using those intermediate goods to produce
![]() $Y_{t}^{*}$
units of the finished good according to the economy’s technology. The first-order condition for the social planner’s problem can be expressed by the equation,
$Y_{t}^{*}$
units of the finished good according to the economy’s technology. The first-order condition for the social planner’s problem can be expressed by the equation,
based on Kydland and Prescott (Reference Kydland and Prescott1982). Appendix A.3 derives (23).
Since technology shocks are a main driving force to efficient business cycle fluctuations, policy stabilization should not target those fluctuations. By definition, the output gap is expressed by:
2.1.6. The central bank
The monetary base consists of currency in circulation,
![]() $N_{t}$
, and reserves,
$N_{t}$
, and reserves,
![]() $N_{t}^{v}$
,
$N_{t}^{v}$
,
where
![]() $N_{t}^{v}=\tau _{t}D_{t}$
. Denote the inflation rate and output growth rate as below:
$N_{t}^{v}=\tau _{t}D_{t}$
. Denote the inflation rate and output growth rate as below:
We assume the central bank imposes monetary policy based on the modified and simplified Taylor rule:
where
![]() $\varepsilon _{rt}$
can be defined as a monetary policy shock.
$\varepsilon _{rt}$
can be defined as a monetary policy shock.
2.1.7. Monetary aggregation
The traditional simple sum monetary aggregate, published by most central banks, is
which can track the true aggregation-theoretic monetary service flow, if and only if the two components are perfectly substitutable. However, this assumption has been unrealistic since the 1950s. Therefore, the necessity of introducing monetary aggregates derived from aggregation theory has emerged. See, for example, Barnett (Reference Barnett1978), Barnett (Reference Barnett1980), and Barnett et al. (Reference Barnett, Chauvet, Leiva-Leon and Su2023) regarding Divisia monetary aggregation.
The monetary aggregate
![]() $M_{t}^{A}$
in equation (8) includes monetary services provided by credit card transactions, as in Barnett et al. (Reference Barnett, Chauvet, Leiva-Leon and Su2023), along with Barnett and Liu (Reference Barnett and Liu2019), Barnett and Park (Reference Barnett and Park2024), Barnett and Park (Reference Barnett and Park2023), Barnett and Su (Reference Barnett and Su2016, Reference Barnett and Su2018), Liu and Serletis (Reference Liu and Serletis2020, Reference Liu and Serletis2022), and Liu, et al. (Reference Liu, Dery and Serletis2020). The opportunity cost of holding monetary assets instead of bonds is given by equation (30), which can be viewed as the price dual of the CES quantity aggregator function (8):
$M_{t}^{A}$
in equation (8) includes monetary services provided by credit card transactions, as in Barnett et al. (Reference Barnett, Chauvet, Leiva-Leon and Su2023), along with Barnett and Liu (Reference Barnett and Liu2019), Barnett and Park (Reference Barnett and Park2024), Barnett and Park (Reference Barnett and Park2023), Barnett and Su (Reference Barnett and Su2016, Reference Barnett and Su2018), Liu and Serletis (Reference Liu and Serletis2020, Reference Liu and Serletis2022), and Liu, et al. (Reference Liu, Dery and Serletis2020). The opportunity cost of holding monetary assets instead of bonds is given by equation (30), which can be viewed as the price dual of the CES quantity aggregator function (8):
This result can be viewed as an extension of Belongia and Ireland (Reference Belongia and Ireland2014) to include credit card services.
Below are the formulas for the user costs of the true monetary aggregate, of currency, of deposits, and of credit card transactions, respectively, as originated by Barnett (Reference Barnett1978), Barnett (Reference Barnett1980), Barnett and Su (Reference Barnett and Su2016, Reference Barnett and Su2018), and Barnett et al. (Reference Barnett, Chauvet, Leiva-Leon and Su2023):
Total expenditure on monetary services is
which can be expressed by:
The expenditure shares of currency, deposits, and credit card transaction services, respectively, are
The growth rate of the credit-augmented Divisia quantity index of monetary services, based upon the Törnqvist-Theil discrete time approximation to the continuous time Divisia index, can be written as:
where the
![]() $\mu$
terms are as defined below for currency, deposits, and credit card transaction services, respectively:
$\mu$
terms are as defined below for currency, deposits, and credit card transaction services, respectively:
The growth rate formula corresponding to (41), (42), and (43) for the Divisia price aggregate of monetary services is
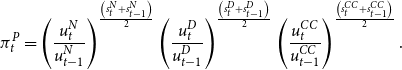 \begin{equation} \pi _{t}^{P}=\left(\frac{u_{t}^{N}}{u_{t-1}^{N}}\right)^{\frac{\left(s_{t}^{N}+s_{t-1}^{N}\right)}{2}}\left(\frac{u_{t}^{D}}{u_{t-1}^{D}}\right)^{\frac{\left(s_{t}^{D}+s_{t-1}^{D}\right)}{2}}\left(\frac{u_{t}^{CC}}{u_{t-1}^{CC}}\right)^{\frac{\left(s_{t}^{CC}+s_{t-1}^{CC}\right)}{2}}. \end{equation}
\begin{equation} \pi _{t}^{P}=\left(\frac{u_{t}^{N}}{u_{t-1}^{N}}\right)^{\frac{\left(s_{t}^{N}+s_{t-1}^{N}\right)}{2}}\left(\frac{u_{t}^{D}}{u_{t-1}^{D}}\right)^{\frac{\left(s_{t}^{D}+s_{t-1}^{D}\right)}{2}}\left(\frac{u_{t}^{CC}}{u_{t-1}^{CC}}\right)^{\frac{\left(s_{t}^{CC}+s_{t-1}^{CC}\right)}{2}}. \end{equation}
2.2. Calibration
The setting of the parameters under the New Keynesian framework follows the benchmark studies of Kydland and Prescott (Reference Kydland and Prescott1982) and Belongia and Ireland (Reference Belongia and Ireland2014). The discount factor of the representative household,
![]() $\beta$
= 0.99, is comparable with a long-run annual interest rate of 4%. Setting
$\beta$
= 0.99, is comparable with a long-run annual interest rate of 4%. Setting
![]() $\eta$
= 2.5 is consistent with a steady-state value of hours worked by the representative agent of 8 hours per day. The setting of
$\eta$
= 2.5 is consistent with a steady-state value of hours worked by the representative agent of 8 hours per day. The setting of
![]() $\theta$
= 6 makes the steady-state markup of price over marginal cost to be 0.2 with monopolistically competitive markets for the differentiated intermediate goods. For the speed of price adjustment in this model, setting
$\theta$
= 6 makes the steady-state markup of price over marginal cost to be 0.2 with monopolistically competitive markets for the differentiated intermediate goods. For the speed of price adjustment in this model, setting
![]() $\phi$
= 50 with quadratic price adjustment costs closely corresponds with Calvo (Reference Calvo1983) pricing when individual goods prices are adjusted every 3.75 quarters on average (Ireland (Reference Ireland2004)). Rotemberg’s quadratic adjustment cost and Calvo’s pricing are distinct; the long-run relationship between inflation and output is positive in the Rotemberg model and negative in the Calvo model. Ireland (Reference Ireland2004) mentions that when utility is nonseparable, the nominal price rigidity follows Calvo’s staggering specification instead of the quadratic adjustment cost specification. The shopping time form is quadratic by setting
$\phi$
= 50 with quadratic price adjustment costs closely corresponds with Calvo (Reference Calvo1983) pricing when individual goods prices are adjusted every 3.75 quarters on average (Ireland (Reference Ireland2004)). Rotemberg’s quadratic adjustment cost and Calvo’s pricing are distinct; the long-run relationship between inflation and output is positive in the Rotemberg model and negative in the Calvo model. Ireland (Reference Ireland2004) mentions that when utility is nonseparable, the nominal price rigidity follows Calvo’s staggering specification instead of the quadratic adjustment cost specification. The shopping time form is quadratic by setting
![]() $\chi$
= 2. Substitutability among monetary assets in the CES aggregator function is determined by the setting
$\chi$
= 2. Substitutability among monetary assets in the CES aggregator function is determined by the setting
![]() $\omega$
= 1.5. The value z = 1.005 supports 2% of the annual growth of real variables in the model. The target value of
$\omega$
= 1.5. The value z = 1.005 supports 2% of the annual growth of real variables in the model. The target value of
![]() $\pi$
= 1.005 implies 2% steady-state annual inflation rate.
$\pi$
= 1.005 implies 2% steady-state annual inflation rate.
A setting of
![]() $v$
= 0.252 makes the steady-state ratio of aggregate monetary service provision to nominal consumption expenditures in the model equal to 2.68. This setting is comparable with a value of 2.61 for the ratio of monetary services provided by currency, deposits, and credit card transactions to quarterly personal consumption expenditure in the U.S. from 2000 to 2018. The 2019 Federal Reserve Payments Study provides the trend in non-cash payments, including credit cards payments. For the composition of monetary service provider components, settings of
$v$
= 0.252 makes the steady-state ratio of aggregate monetary service provision to nominal consumption expenditures in the model equal to 2.68. This setting is comparable with a value of 2.61 for the ratio of monetary services provided by currency, deposits, and credit card transactions to quarterly personal consumption expenditure in the U.S. from 2000 to 2018. The 2019 Federal Reserve Payments Study provides the trend in non-cash payments, including credit cards payments. For the composition of monetary service provider components, settings of
![]() $\nu$
= 0.19 and
$\nu$
= 0.19 and
![]() $\xi$
= 0.60 induces the steady-state ratio of currency
$\xi$
= 0.60 induces the steady-state ratio of currency
![]() $N_{t}$
, deposits
$N_{t}$
, deposits
![]() $D_{t}$
, and credit cards transactions
$D_{t}$
, and credit cards transactions
![]() $CC_{t}$
to be 10.7, 87.2, and 1.98, respectively. Data from the CFS show that the average ratio among them is 10.3, 87.7, and 2.0, respectively, using monetary data from July 2006 to May 2021.
$CC_{t}$
to be 10.7, 87.2, and 1.98, respectively. Data from the CFS show that the average ratio among them is 10.3, 87.7, and 2.0, respectively, using monetary data from July 2006 to May 2021.
Setting
![]() $\tau$
= 0.05 is consistent with the average ratio of total reserves to the deposit component of M2 (excluding currency), as calculated from the FRED database data from January 1959 to December 2019. Considering the Fed has decided to provide interest on reserves since 2008, the value has been skyrocketing from 0.05 to 0.1493 (Section 3.1.1 narrows the data period from July 2006 to December 2019 and calibrates the
$\tau$
= 0.05 is consistent with the average ratio of total reserves to the deposit component of M2 (excluding currency), as calculated from the FRED database data from January 1959 to December 2019. Considering the Fed has decided to provide interest on reserves since 2008, the value has been skyrocketing from 0.05 to 0.1493 (Section 3.1.1 narrows the data period from July 2006 to December 2019 and calibrates the
![]() $\tau$
value of 0.1493). The setting
$\tau$
value of 0.1493). The setting
![]() $x$
= 0.0115 implies that 2.61% of the steady-state total aggregate output can be explained by banking activity, with deposit costs measured in units of the finished good. To support this setting, the annual data from FRED for 2001 to 2016 show that the ratio to GDP of Federal Reserve banks, credit intermediation, and related services for U.S. metropolitan portion is 2.79. Additionally, the data from the BEA indicate that the ratio of Federal Reserve banks, credit intermediation, and related activities to GDP is 2.72 from 1997 to 2019.
$x$
= 0.0115 implies that 2.61% of the steady-state total aggregate output can be explained by banking activity, with deposit costs measured in units of the finished good. To support this setting, the annual data from FRED for 2001 to 2016 show that the ratio to GDP of Federal Reserve banks, credit intermediation, and related services for U.S. metropolitan portion is 2.79. Additionally, the data from the BEA indicate that the ratio of Federal Reserve banks, credit intermediation, and related activities to GDP is 2.72 from 1997 to 2019.
Equation (18) explains the relationship between credit card transaction volumes and deposits. The setting
![]() $\varpi$
= 0.0228 supports the ratio of credit card transaction services to deposits, with that ratio calculated from monthly CFS data for July 2006 to May 2021. Meanwhile, the 2019 Federal Reserve Payments Study supports the fact that the ratio of credit card payments to total non-cash payments equals 0.029 on annual average from 2000 to 2018.
$\varpi$
= 0.0228 supports the ratio of credit card transaction services to deposits, with that ratio calculated from monthly CFS data for July 2006 to May 2021. Meanwhile, the 2019 Federal Reserve Payments Study supports the fact that the ratio of credit card payments to total non-cash payments equals 0.029 on annual average from 2000 to 2018.
For the value of the benchmark parameters, we set
![]() $\rho _{r}$
= 0.75 and
$\rho _{r}$
= 0.75 and
![]() $\rho _{\pi }$
= 0.3 to obtain the observed smoothness of interest rates, while
$\rho _{\pi }$
= 0.3 to obtain the observed smoothness of interest rates, while
![]() $\rho _{v}$
= 0.95 and
$\rho _{v}$
= 0.95 and
![]() $\rho _{a}$
= 0.9 are consistent with the money demand and preference shocks being highly persistent. The parameter settings of
$\rho _{a}$
= 0.9 are consistent with the money demand and preference shocks being highly persistent. The parameter settings of
![]() $\rho _{x}$
= 0.5 and
$\rho _{x}$
= 0.5 and
![]() $\rho _{\tau }$
= 0.5 are consistent with the effects of financial cost shocks and reserve shocks decaying quickly compared to other shocks. Finally, the setting
$\rho _{\tau }$
= 0.5 are consistent with the effects of financial cost shocks and reserve shocks decaying quickly compared to other shocks. Finally, the setting
![]() $\rho _{\varpi }$
= 0.8 implies that the shock of credit usage behavior is persistent compared to the reserve shock and financial cost shock.
$\rho _{\varpi }$
= 0.8 implies that the shock of credit usage behavior is persistent compared to the reserve shock and financial cost shock.
The standard deviation of the innovations to each shock are given by different scales, where
![]() $\sigma _{v}$
= 0.01,
$\sigma _{v}$
= 0.01,
![]() $\sigma _{a}$
= 0.01, and
$\sigma _{a}$
= 0.01, and
![]() $\sigma _{z}$
= 0.01 explain the general cases of innovation. To simulate the financial crisis, we set the extreme values of
$\sigma _{z}$
= 0.01 explain the general cases of innovation. To simulate the financial crisis, we set the extreme values of
![]() $\sigma _{\tau }$
= 1,
$\sigma _{\tau }$
= 1,
![]() $\sigma _{x}$
= 0.25, and
$\sigma _{x}$
= 0.25, and
![]() $\sigma _{\varpi }$
= 1. By doing so, we can track what happens to the impulse responses to reserve shocks, when the bank’s demand for reserves doubles. The setting
$\sigma _{\varpi }$
= 1. By doing so, we can track what happens to the impulse responses to reserve shocks, when the bank’s demand for reserves doubles. The setting
![]() $\sigma _{r}$
= 0.0025 is consistent with how the monetary policy shock affects the short-term nominal interest rate.
$\sigma _{r}$
= 0.0025 is consistent with how the monetary policy shock affects the short-term nominal interest rate.
2.3. Results
Figures 1 and 2 provide justification for using credit-augmented Divisia instead of simple sum. Figures 1 and 2 show the impulse responses of the growth rates of three different monetary aggregates: the theoretical monetary aggregate (8), credit-augmented Divisia (40), and the simple sum monetary aggregate (29), to seven different exogenous shocks. The results in these figures can answer the question, does measurement still matter in a New Keynesian world? In short, the answer to the question in this framework is “yes,” especially if we expand the scope of the monetary services to include deferred payment credit card transactions. The first and second columns of Figures 1 and 2 demonstrate that the impulse responses of credit-augmented Divisia perfectly track those of the true monetary aggregate for all types of shocks, even in a New Keynesian model. We can trace the fact that their values are the same to the fourth decimal place.
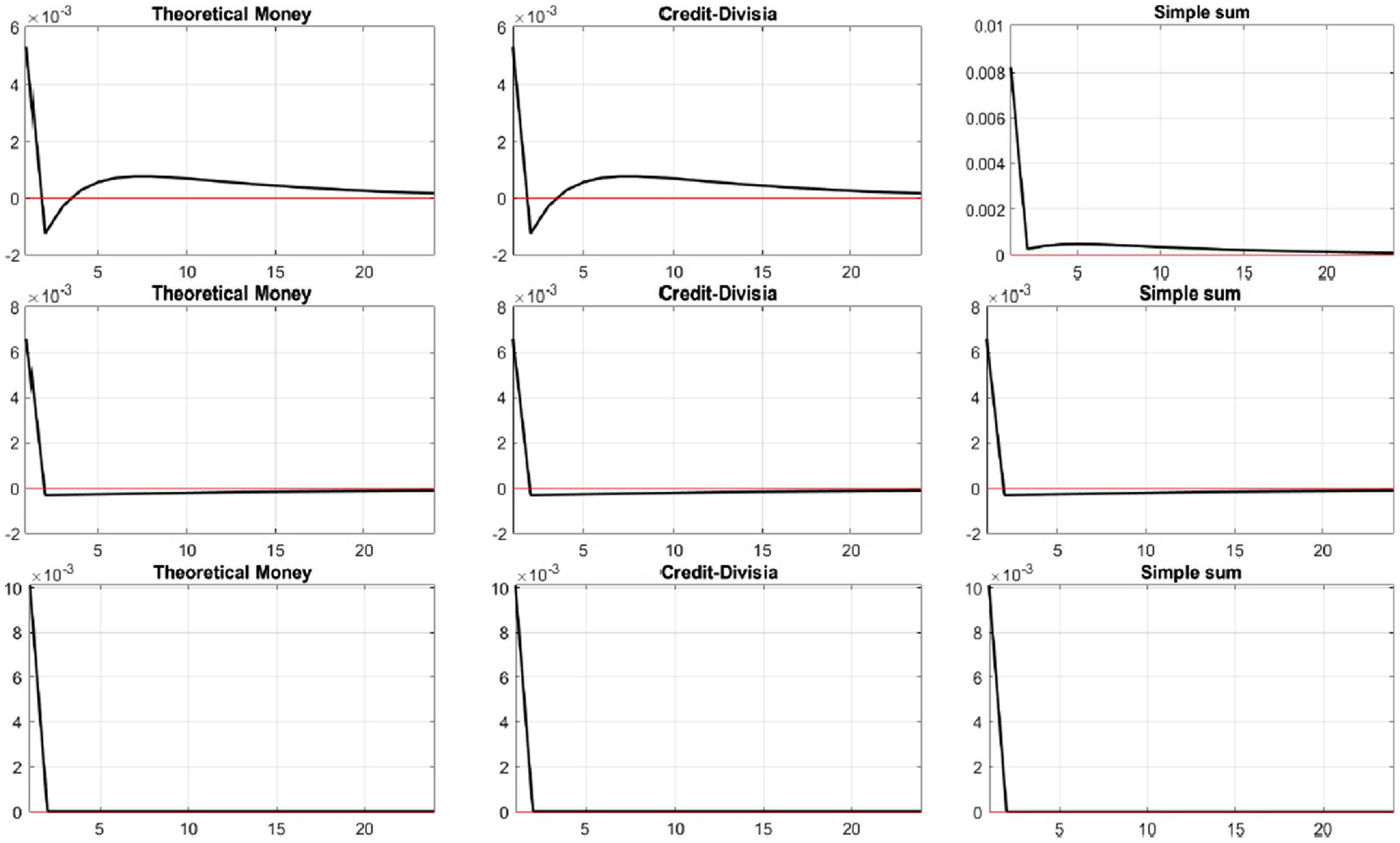
Figure 1. Impulse responses for nominal money growth. First row: Preference shock. Second row: Money demand shock. Third row: Technology shock.
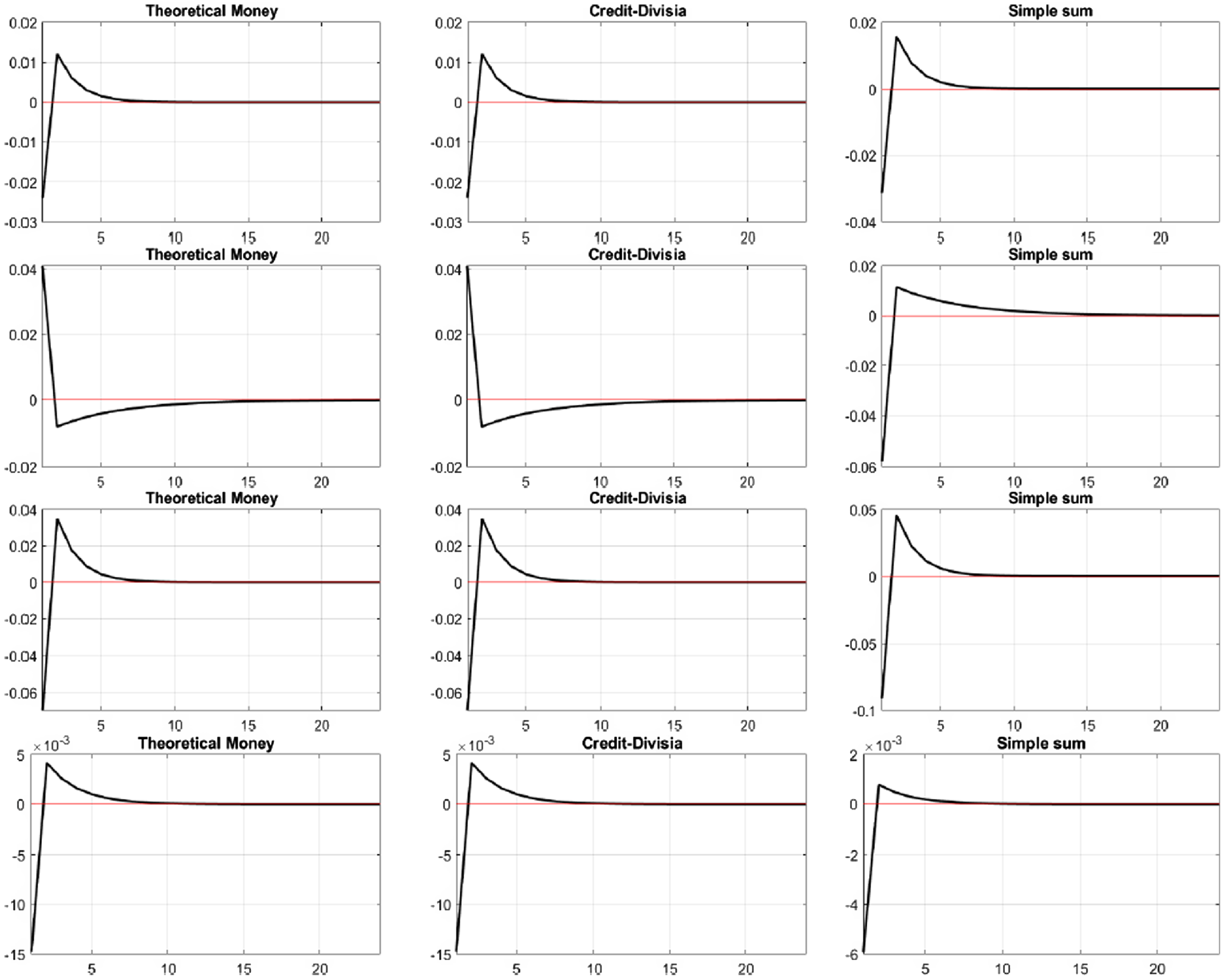
Figure 2. Impulse responses for nominal money growth. First row: Reserve ratio shock. Second row: Credit-deposit shock. Third row: Financial cost shock. Fourth row: Monetary policy shock.
However, considering the third column, the impulse responses of simple sum are substantially different from those of true money. We can directly grasp the difference of responses to preference shocks (Figure 1, row 1), credit-deposit shocks (Figure 2, row 2), and monetary policy shocks (Figure 2, row 4). In the last row of Figure 2, the decline of the growth rates of the true and credit-augmented Divisia are greater than that of the simple sum monetary aggregate. The results in these figures support the importance of the monetary measurement tools as Belongia and Ireland (Reference Belongia and Ireland2014) first asserted in a New Keynesian context.
Figures 3 and 4 provide the impulse responses of macroeconomic variables to seven shocks. Our objective in these figures is to investigate whether the behaviors of impulse responses are consistent with the basic logic of the New Keynesian framework, when we introduce credit card services. We focus on the behavior of output, inflation rate, and interest rate.
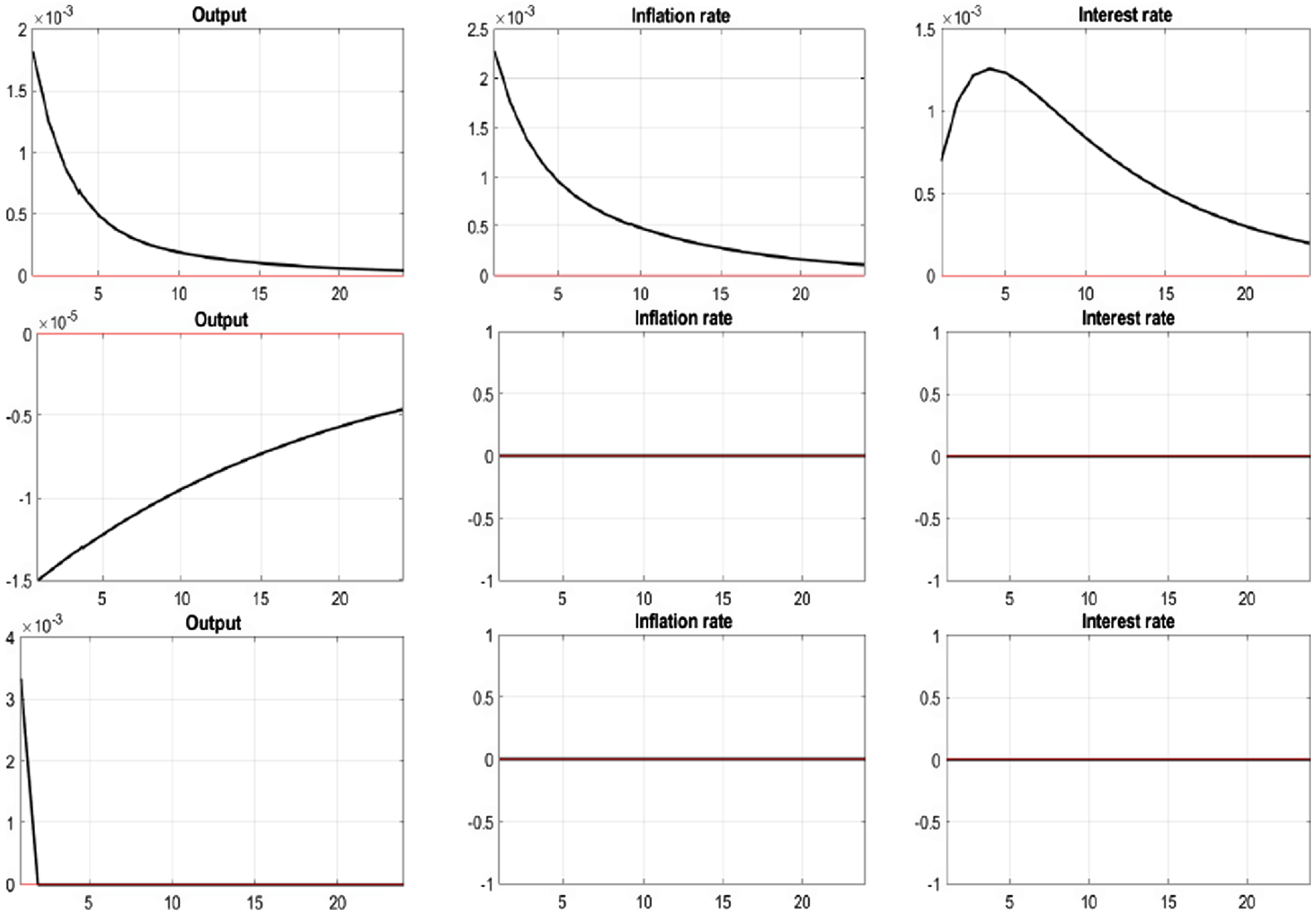
Figure 3. Impulse responses for macroeconomic variables; 1st row: Preference shock, 2nd row: Money demand shock, 3rd row: Technology shock.
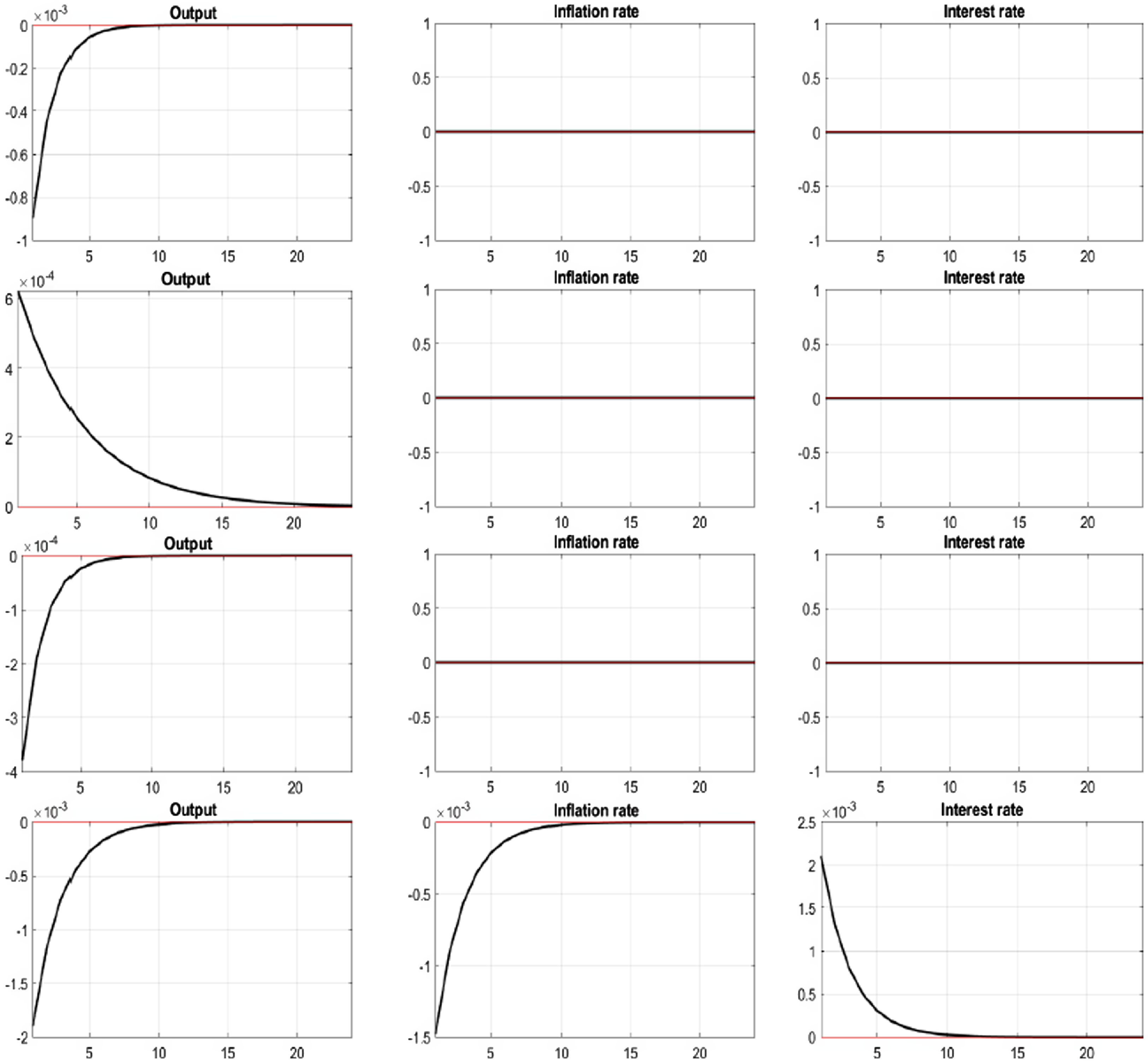
Figure 4. Impulse responses for macroeconomic variables; 1st row: Reserve ratio shock, 2nd row: Credit-deposit shock, 3rd row: Financial cost shock, 4th row: Monetary policy shock.
The first row of Figure 3 provides the impulse responses to preference shocks inducing increases of output and inflation rate. The parameter settings of the modified Taylor rule,
![]() $\rho _{r}$
= 0.75 and
$\rho _{r}$
= 0.75 and
![]() $\rho _{\pi }$
= 0.3, require continuous monetary tightening to offset economic overheating. The result implies that the preemptive policy for inflation would stabilize the economy successfully. The second row of Figure 3 shows the impulse responses to the money demand shocks. By maintaining the nominal interest rate at a fixed level, the modified Taylor rule requires the monetary authority to implement the policy that increases the money supply to produce stable output and inflation. The third row of Figure 3 provides the impulse response to the technology shock. Since the technology shock follows a random walk with drift, we would expect a permanent increase in productivity.
$\rho _{\pi }$
= 0.3, require continuous monetary tightening to offset economic overheating. The result implies that the preemptive policy for inflation would stabilize the economy successfully. The second row of Figure 3 shows the impulse responses to the money demand shocks. By maintaining the nominal interest rate at a fixed level, the modified Taylor rule requires the monetary authority to implement the policy that increases the money supply to produce stable output and inflation. The third row of Figure 3 provides the impulse response to the technology shock. Since the technology shock follows a random walk with drift, we would expect a permanent increase in productivity.
However, the result shows that the effect of the technology shock to output converges to zero after the initial shock. The reason appears to be our adoption of a stationary system. As a result, the 11 real variables, including output, the 9 money stock variables, and the 2 price variables are normalized by the technology shock,
![]() $Z_{t}$
. The resulting full stationary system is provided in Appendix B.1.
$Z_{t}$
. The resulting full stationary system is provided in Appendix B.1.
In Figure 4, the first and third rows display the response to reserve ratio shocks and financial cost shocks, respectively. When the shocks are imposed, the inflation rate remains unchanged, while the output decreases. Again, under the modified Taylor rule, these two types of shocks put pressure on the central bank to accommodate increased demand for money to stabilize the price level. Observing the large decrease in the theoretical monetary aggregate and credit-augmented Divisia in Figure 2, we conclude that the increase in the monetary base implemented by the monetary policy is not adequate to cover the change in the monetary base caused by the impact of the financial sector shock. The decreasing liquidity induces a decrease in output, as shown in Figure 4 again.
The second row of Figure 4 provides the response to the credit usage behavior shock. Since credit card transactions contribute to liquidity services in the form of deferred payment services, a positive shock causes an increase in credit-augmented Divisia in Figure 2. Finally, the shock induces an increase in output. The last row of Figure 4 explains the effect of monetary policy shocks. Following monetary tightening, output and inflation rate decrease. The amount of the inflation rate decrease is smaller than that of output. As a result, nominal price rigidity induces monetary non-neutrality in the short run. Compared to the impulse response of the theoretical monetary aggregate and of output, we can track the liquidity effect clearly, since its fluctuation is larger than that of output.Footnote 6
3. Empirical approach
The purpose of this section is to study the empirical performance of the credit-augmented Divisia monetary aggregate. By adopting credit-augmented Divisia as a monetary variable in the recursive VAR model, we investigate whether the empirical results with VAR are consistent with those of the calibrated DSGE New Keynesian model in the previous section. We expect that the empirical usefulness of credit-augmented Divisia would be confirmed, if common behaviors are observed by comparing the impulse response of the main variables in the DSGE structure with those in the VAR. Since the CFS publishes credit-augmented Divisia data monthly from July 2006, we focus only on the period from July 2006 to December 2019 for both approaches.Footnote 7 The period includes the Great Recession and the ZLB period. However, we do not include the very abnormal COVID-19 pandemic era. We track the behavior of the impulse response to the monetary policy shock induced by the modified Taylor rule.
Next, we evaluate the effectiveness of credit-augmented Divisia as a monetary policy indicator by using a recursive VAR. Traditionally, the effective federal funds rate has played an important role as an indicator. However, since the behavior of the federal funds rate at the lower bound was not adequate to explain the economic phenomena, alternatives have been introduced, such as the shadow federal funds rate (Wu and Xia (Reference Wu and Xia2016). We investigate whether credit-augmented Divisia can be a good alternative as a monetary policy indicator. To do so, we replace the federal funds rate data with monetary aggregate data in the VAR. This method has previously been suggested by Christiano et al. (Reference Christiano, Eichenbaum and Evans1999) with simple sum M1 and M2 as policy indicators. Keating et al. (Reference Keating, Kelly, Smith and Valcarcel2019) expanded that study by introducing the broader Divisia monetary aggregate M4 (DM4) as a substitute for the federal funds rate. We will consider credit-augmented Divisia M2 as a candidate for monetary policy indicator. We do not consider credit-augmented Divisia M4, since properly consolidated simple sum M4 is not currently available for comparison from any sources.
3.1. DSGE New Keynesian model revisited
3.1.1. Calibration
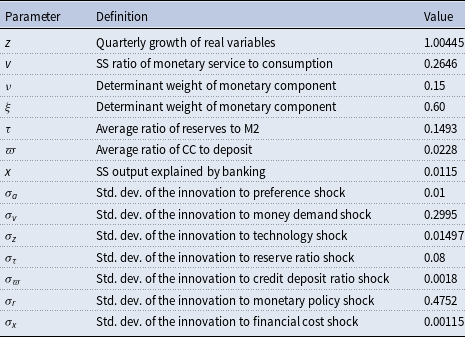
First, we adopt the DSGE New Keynesian model from the previous section and apply a new calibration relevant to the limited time period. Table 1 displays the newly calibrated parameters, and Appendix C explains the choices in detail. While the setting for
![]() $\tau$
is increased to match the higher level of reserves relative to deposits, the model continues for simplicity to assume that reserves do not pay interest. In future work, it could be useful to extend the analysis from this paper to account for interest payment on reserves, perhaps along the same line as Ireland (Reference Ireland2014).
$\tau$
is increased to match the higher level of reserves relative to deposits, the model continues for simplicity to assume that reserves do not pay interest. In future work, it could be useful to extend the analysis from this paper to account for interest payment on reserves, perhaps along the same line as Ireland (Reference Ireland2014).
Table 1. Parameter calibration (July 2006 to December 2019)
We choose the impulse response of five key variables to monetary policy shocks: output, inflation, interest rate, credit-augmented Divisia, and monetary base. The results are displayed in the first column of Figure 5.
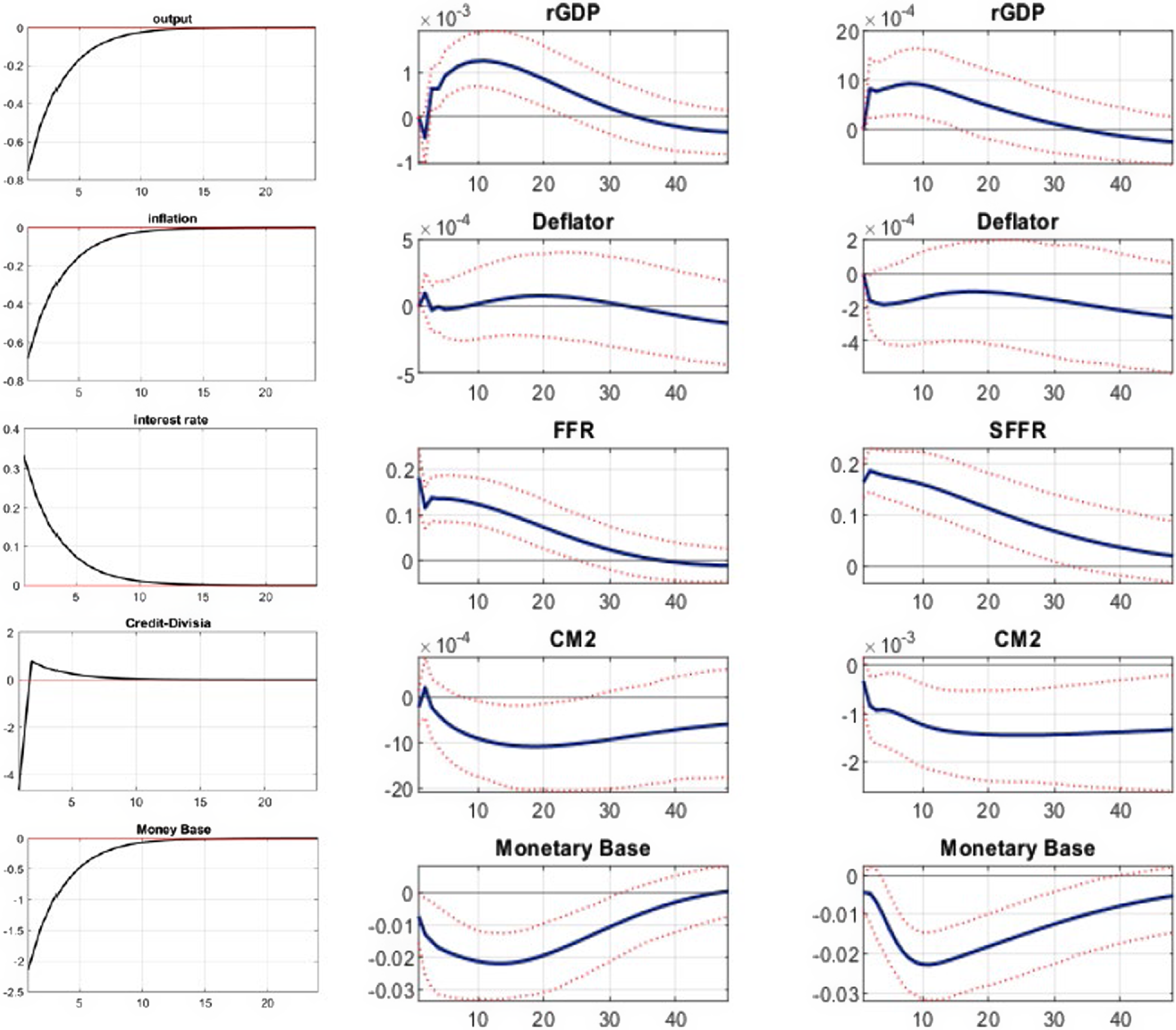
Figure 5. Impulse response for economic variables to monetary policy shock. First column: DSGE model; second column: VAR model with effective federal funds rate; third column: VAR model with shadow federal funds rate.
3.2. VAR estimation
The reduced form VAR model, as in Sims (Reference Sims1980), is:
where
![]() $p$
is the number of lags, with
$p$
is the number of lags, with
![]() $\mathbf{u}_{t}$
assumed to be serially uncorrelated disturbances having covariance matrix,
$\mathbf{u}_{t}$
assumed to be serially uncorrelated disturbances having covariance matrix,
![]() $\mathrm{\mathbb{E}}(\mathbf{u}_{t}\mathbf{u}_{t}')=\mathbf{V}$
. The reduced form VAR disturbances are related to the underlying structural economic shocks,
$\mathrm{\mathbb{E}}(\mathbf{u}_{t}\mathbf{u}_{t}')=\mathbf{V}$
. The reduced form VAR disturbances are related to the underlying structural economic shocks,
![]() $\mathbf{\varepsilon }_{t}$
, by
$\mathbf{\varepsilon }_{t}$
, by
where,
![]() $\mathbf{\varepsilon }_{t}$
is serially uncorrelated white noise with a diagonal covariance matrix
$\mathbf{\varepsilon }_{t}$
is serially uncorrelated white noise with a diagonal covariance matrix
![]() $\mathbf{\Sigma }_{\mathbf{\varepsilon }}$
of full rank, and
$\mathbf{\Sigma }_{\mathbf{\varepsilon }}$
of full rank, and
![]() $\mathbf{B}_{0}$
is a lower triangular matrix. Substituting (46) into the VAR equation (45) and multiplying by
$\mathbf{B}_{0}$
is a lower triangular matrix. Substituting (46) into the VAR equation (45) and multiplying by
![]() $\mathbf{B}_{0}^{-1}$
on both sides, we get
$\mathbf{B}_{0}^{-1}$
on both sides, we get
We determined the relationship
![]() $\mathbf{V}=\mathbf{B}_{0}\mathbf{B}_{0}'$
by using the Cholesky decomposition. The order of the variables becomes important, when we impose the zero restriction with the Cholesky decomposition. There is no fixed rule for the variable ordering, but conventionally the most exogenous variable is located in the first row of the vector
$\mathbf{V}=\mathbf{B}_{0}\mathbf{B}_{0}'$
by using the Cholesky decomposition. The order of the variables becomes important, when we impose the zero restriction with the Cholesky decomposition. There is no fixed rule for the variable ordering, but conventionally the most exogenous variable is located in the first row of the vector
![]() $\mathbf{Y}_{t}$
, and the least exogenous variable is located in the last row of the vector.
$\mathbf{Y}_{t}$
, and the least exogenous variable is located in the last row of the vector.
We introduce 6 variables with monthly frequency in the VAR model. The real GDP data are collected from IHS Markit.Footnote 8 Their monthly real GDP calculations and aggregation methods are comparable to the official GDP data from the U.S. Bureau of Economic Analysis (BEA). Next, the GDP deflator and commodity price follow. Since IHS Markit provides nominal and real GDP in monthly frequency, we can calculate the monthly frequency GDP deflator. These three variables show lagged impulse response to the monetary policy shock. The alternative monetary policy instrument, credit-augmented Divisia M2, is in the following row. For the last row, the monetary base and the user cost of credit-augmented Divisia M2 are located. They are the least exogenous. Finally, we choose the VAR(2) model with constant, since that model produced the lowest AIC and BIC.
3.3. Results
The first column in Figure 5 shows the DSGE impulse responses to contractionary monetary policy shocks for the key economic variables. Output and inflation rate fall immediately and converge to zero. We could conjecture that the temporary drop in the inflation rate induces the price level to decrease and converge to the negative level permanently. Credit-augmented Divisia monetary quantity falls instantaneously, displaying a liquidity effect. The second and third columns display the impulse responses to the monetary policy shock of the key economic variables under the recursive VAR estimation. Each column uses the effective federal funds rate and the shadow federal funds rate as monetary policy indicators, respectively. Unfortunately, we cannot track the common behaviors between the DSGE and empirical results. The output and price puzzles are captured in both empirical results.
Considering credit-augmented Divisia as an alternative policy tool provides a robust result. We consider credit-augmented Divisia M2 as an indicator of a negative monetary policy shock. Figure 6 demonstrates the impulse responses to monetary policy shocks with 90% confidence intervals. Each column possesses various monetary policy indicators in the fourth row. The first and second columns in Figure 6 follow Figure 2 in the Keating et al. (Reference Keating, Kelly, Smith and Valcarcel2019) baseline VAR model, which uses Divisia M4 as a monetary policy indicator. The use of user cost in the last row is based on the fact that macroeconomic models typically include at least one interest rate (Keating et al. (Reference Keating, Kelly, Smith and Valcarcel2019)). The first column uses credit-augmented Divisia M2 as a policy indicator. The response of the output shows the typical behavior. It reaches the lowest point after 2 years and slightly increases toward the origin. Since the initial positive shock is not observed, the output puzzle problem does not exist in this model, and the behavior is statistically significant after 1 year.
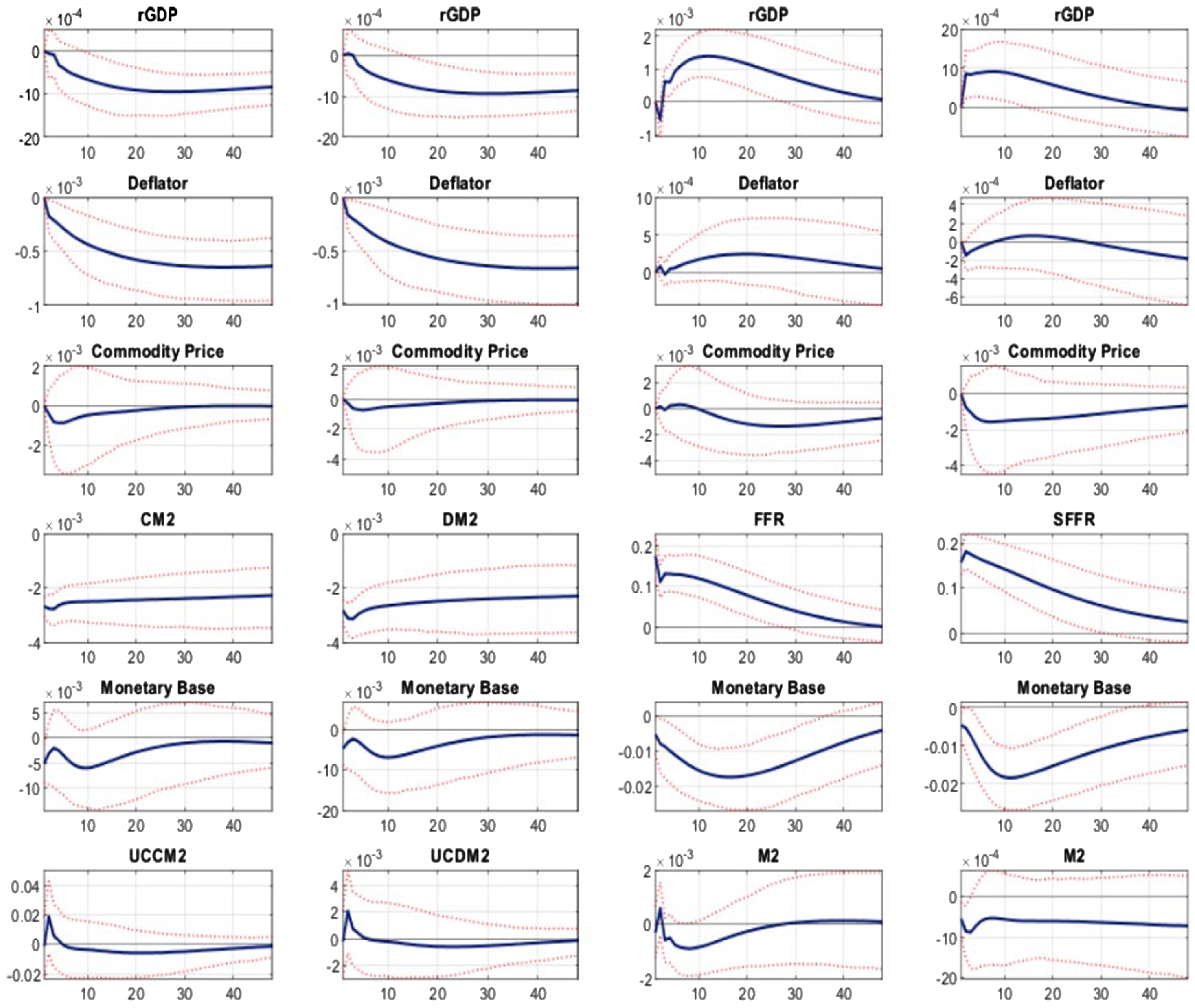
Figure 6. Impulse response to monetary policy shock (Keating et al. (Reference Keating, Kelly, Smith and Valcarcel2019) benchmark).

Figure 7. Impulse response to monetary policy shock (Christiano et al. (Reference Christiano, Eichenbaum and Evans1999) benchmark).
The price level is decreasing and converges to a negative value in the long run. This is a desirable result. Commodity prices show sensitive behavior. They fall faster than the price level but converge to zero instantly. The monetary base and the user cost of credit-augmented Divisia M2 are the least exogenous. The monetary base drops immediately and remains at its negative value with a statistically insignificant interval. In the last row, the user cost increases at the initial period and converges to the origin in the short run. The results in the first column are consistent with those of the theoretical model explained in the first column of Figure 5. Moreover, the model is not contaminated by the output, price, and liquidity puzzles.
For the third and fourth columns in Figure 6, we benchmark the additional VAR estimation of Keating et al. (Reference Keating, Kelly, Smith and Valcarcel2019), Figure 6, shadow rate VAR models. Keating et al. (Reference Keating, Kelly, Smith and Valcarcel2019) adopt the federal funds rate and the shadow federal funds rate as monetary policy indicators, and the simple sum monetary aggregate in the last row as proxy for user cost. The third and fourth columns show the impulse responses when the federal funds rate and shadow federal funds rate are considered as monetary policy tools, respectively. The most noticeable result is that the puzzle problems of output and price level last more than 2 years. Meanwhile, liquidity puzzle problems are not detected in both cases.
The use of a Divisia monetary aggregate as an alternative monetary policy indicator above is consistent with Keating et al. (Reference Keating, Kelly, Smith and Valcarcel2019), while the use of an M2-level monetary aggregate is consistent with Christiano et al. (Reference Christiano, Eichenbaum and Evans1999). The results below, following Christiano et al. (Reference Christiano, Eichenbaum and Evans1999), support our conclusion that considering credit-augmented Divisia M2 as an alternative policy indicator produces robust favorable results.
Figure 7 displays the impulse responses using various monetary policy indicators. Credit-augmented Divisia M2 is in the first column, while the federal funds rate and shadow federal funds rate are in the third and the last columns, respectively. We observe different dynamics for each column. In the first column, the output puzzle is observed in the short term, but the price puzzle is not observed. However, the responses for the other indicators are not free from either the output or price puzzle, and their positive responses last more than 3 years.
The fifth to seventh rows show the response of the variables related to liquidity. The behavior of non-borrowed reserves depicted in the first, third, fourth columns show initial fluctuations. After 18 months, the responses reach their lowest point, and later they converge to zero. For the response of total reserves, three cases commonly experience a positive spark at the initial period and touch their lowest point after 1 year. The response of the first column converges to zero relatively faster than their counterparts. The impulse response of M2 is consistently negative, when credit-augmented Divisia M2 is considered as an indicator. However, in the case of its counterparts, M2 shows initial fluctuations and converges to zero after experiencing a positive effect. That result is not free from the liquidity puzzle.
Based on the results in Figures 6 and 7, we conclude that credit-augmented Divisia M2 can be considered as a good alternative policy indicator and provides clearer economic implications than the alternatives we have considered. Furthermore, the empirical results are comparable to and consistent with the DSGE New Keynesian model, described in the first column of Figure 5.
4. Conclusion
Do credit card services matter? Does the Barnett Critique matter? Positive answers to both questions are consistent with the results of this paper. Since the original Divisia monetary aggregates were introduced, many researchers have shown the theoretical and empirical superiority of the Divisia-type monetary aggregates compared to the simple sum. Belongia’s work (Reference Belongia1996) further confirms this conclusion and emphasizes the importance of the correct data consistent with economic aggregation theory. Hence Belongia (Reference Belongia1996) argues “Measurement Matters.”
In this study, we introduce credit-augmented Divisia into a DSGE New Keynesian model having imperfect markets. The purpose of this research is to compare the credit-augmented Divisia with simple sum. The credit-augmented monetary aggregate incorporates the deferred payments services of credit cards into an aggregate also including services of monetary assets. But removing the credit card services from the aggregate in our New Keynesian model to produce a Divisia aggregate containing only monetary assets would not be consistent with economic aggregation theory, since we find that removing the credit card services would violate the weak separability condition necessary for existence of an aggregator function.
Prior research on inclusion of credit card services within a Divisia monetary aggregate in perfect markets has not precluded removal of the credit card services from within the aggregate. But we find that our New Keynesian imperfect market assumptions could preclude removal of the credit card services. Hence, we have not only provided empirical results supporting inclusion of credit card services into Divisia monetary aggregates, but also a New Keynesian theoretical reason emphasizing an interaction between credit card services and monetary deposit services not permitting removal of the credit card services without violation of the fundamental existence condition for quantity aggregation.
Our empirical results explore both the tracking ability of the credit-augmented Divisia monetary aggregate relative to the theoretical aggregator function and implications of impulse responses in a VAR model. We compare with other indicators, including Federal Funds rates and simple sum monetary aggregates. We emphasize M2, since that is the broadest monetary aggregate for which properly consolidate simple sum aggregates are currently available for comparison. In addition, the choice of M2 permits comparison with Christiano et al. (Reference Christiano, Eichenbaum and Evans1999). However, we believe that credit-augmented Divisia M3 or M4 aggregates might perform even better than credit-augmented Divisia M2.
By interpreting impulse responses to various types of shocks, we demonstrate that similarity and consistency can be observed between the behavior of the aggregation-theoretic exact monetary aggregate and credit-augmented Divisia. Furthermore, the behavior of the impulse responses of economic variables retain the basic properties of New Keynesian framework. These results are consistent with the benchmark paper, Belongia and Ireland (Reference Belongia and Ireland2014), which introduced original Divisia into the DSGE New Keynesian model.
Considering the credit-augmented Divisia as an alternative monetary policy instrument provides robust economic implications solving critical puzzles in the literature, including the output, price and liquidity puzzles. We also find consistency between the results with empirical VAR and those with our calibrated DSGE New Keynesian model. With the growing relevance of deferred payment credit card services in transactions and with the increasing importance New Keynesian DSGE models, we conclude that the new credit-card-augmented Divisia monetary aggregates provide an important step forward in methodology and potential applications.
Appendix
A. Optimization Problems
A.1. Household optimization
The household optimization problem with shopping time model starts from the utility function:
with three constraints (definition of deposit, true monetary aggregation, and currency) to be carried over to the next period, divided by the price,
![]() $P_{t}$
, and with free disposal allowed:
$P_{t}$
, and with free disposal allowed:
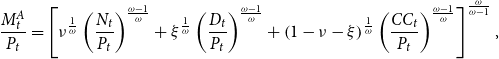 \begin{equation} \frac{M_{t}^{A}}{P_{t}}=\left[\nu ^{\frac{1}{\omega }}\left(\frac{N_{t}}{P_{t}}\right)^{\frac{\omega -1}{\omega }}+\xi ^{\frac{1}{\omega }}\left(\frac{D_{t}}{P_{t}}\right)^{\frac{\omega -1}{\omega }}+\left(1-\nu -\xi \right)^{\frac{1}{\omega }}\left(\frac{CC_{t}}{P_{t}}\right)^{\frac{\omega -1}{\omega }}\right]^{\frac{\omega }{\omega -1}}, \end{equation}
\begin{equation} \frac{M_{t}^{A}}{P_{t}}=\left[\nu ^{\frac{1}{\omega }}\left(\frac{N_{t}}{P_{t}}\right)^{\frac{\omega -1}{\omega }}+\xi ^{\frac{1}{\omega }}\left(\frac{D_{t}}{P_{t}}\right)^{\frac{\omega -1}{\omega }}+\left(1-\nu -\xi \right)^{\frac{1}{\omega }}\left(\frac{CC_{t}}{P_{t}}\right)^{\frac{\omega -1}{\omega }}\right]^{\frac{\omega }{\omega -1}}, \end{equation}
and
By combining these four expressions, we can get the Lagrangian form:
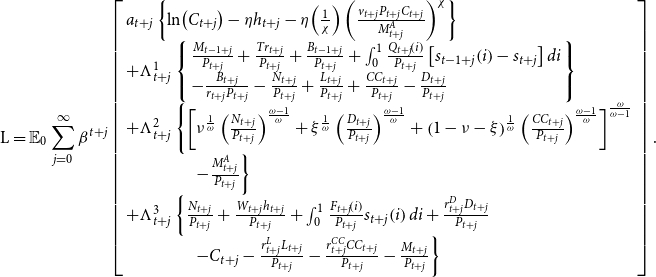 \begin{equation} \mathrm{L}=\mathrm{\mathbb{E}}_{0}\sum _{j=0}^{\infty }\beta ^{t+j}\left[\begin{array}{l} a_{t+j}\left\{\ln\!\left(C_{t+j}\right)-\eta h_{t+j}-\eta\!\left(\frac{1}{\chi }\right)\left(\frac{v_{t+j}P_{t+j}C_{t+j}}{M_{t+j}^{A}}\right)^{\chi }\right\}\\ +\Lambda _{t+j}^{1}\left\{\begin{array}{l} \frac{M_{t-1+j}}{P_{t+j}}+\frac{Tr_{t+j}}{P_{t+j}}+\frac{B_{t-1+j}}{P_{t+j}}+\int _{0}^{1}\frac{Q_{t+j}\!\left(i\right)}{P_{t+j}}\left[s_{t-1+j}\!\left(i\right)-s_{t+j}\right]di\\ -\frac{B_{t+j}}{r_{t+j}P_{t+j}}-\frac{N_{t+j}}{P_{t+j}}+\frac{L_{t+j}}{P_{t+j}}+\frac{CC_{t+j}}{P_{t+j}}-\frac{D_{t+j}}{P_{t+j}} \end{array}\right\}\\ +\Lambda _{t+j}^{2}\left\{\left[\nu ^{\frac{1}{\omega }}\left(\frac{N_{t+j}}{P_{t+j}}\right)^{\frac{\omega -1}{\omega }}+\xi ^{\frac{1}{\omega }}\left(\frac{D_{t+j}}{P_{t+j}}\right)^{\frac{\omega -1}{\omega }}+\left(1-\nu -\xi \right)^{\frac{1}{\omega }}\left(\frac{CC_{t+j}}{P_{t+j}}\right)^{\frac{\omega -1}{\omega }}\right]^{\frac{\omega }{\omega -1}}\right.\\ \left.\qquad\qquad-\frac{M_{t+j}^{A}}{P_{t+j}}\right\}\\ +\Lambda _{t+j}^{3}\left\{\frac{N_{t+j}}{P_{t+j}}+\frac{W_{t+j}h_{t+j}}{P_{t+j}}+\int _{0}^{1}\frac{F_{t+j}\!\left(i\right)}{P_{t+j}}s_{t+j}\!\left(i\right)di+\frac{r_{t+j}^{D}D_{t+j}}{P_{t+j}}\right.\\\qquad\qquad\left.-C_{t+j}-\frac{r_{t+j}^{L}L_{t+j}}{P_{t+j}}-\frac{r_{t+j}^{CC}CC_{t+j}}{P_{t+j}}-\frac{M_{t+j}}{P_{t+j}}\right\} \end{array}\right]. \end{equation}
\begin{equation} \mathrm{L}=\mathrm{\mathbb{E}}_{0}\sum _{j=0}^{\infty }\beta ^{t+j}\left[\begin{array}{l} a_{t+j}\left\{\ln\!\left(C_{t+j}\right)-\eta h_{t+j}-\eta\!\left(\frac{1}{\chi }\right)\left(\frac{v_{t+j}P_{t+j}C_{t+j}}{M_{t+j}^{A}}\right)^{\chi }\right\}\\ +\Lambda _{t+j}^{1}\left\{\begin{array}{l} \frac{M_{t-1+j}}{P_{t+j}}+\frac{Tr_{t+j}}{P_{t+j}}+\frac{B_{t-1+j}}{P_{t+j}}+\int _{0}^{1}\frac{Q_{t+j}\!\left(i\right)}{P_{t+j}}\left[s_{t-1+j}\!\left(i\right)-s_{t+j}\right]di\\ -\frac{B_{t+j}}{r_{t+j}P_{t+j}}-\frac{N_{t+j}}{P_{t+j}}+\frac{L_{t+j}}{P_{t+j}}+\frac{CC_{t+j}}{P_{t+j}}-\frac{D_{t+j}}{P_{t+j}} \end{array}\right\}\\ +\Lambda _{t+j}^{2}\left\{\left[\nu ^{\frac{1}{\omega }}\left(\frac{N_{t+j}}{P_{t+j}}\right)^{\frac{\omega -1}{\omega }}+\xi ^{\frac{1}{\omega }}\left(\frac{D_{t+j}}{P_{t+j}}\right)^{\frac{\omega -1}{\omega }}+\left(1-\nu -\xi \right)^{\frac{1}{\omega }}\left(\frac{CC_{t+j}}{P_{t+j}}\right)^{\frac{\omega -1}{\omega }}\right]^{\frac{\omega }{\omega -1}}\right.\\ \left.\qquad\qquad-\frac{M_{t+j}^{A}}{P_{t+j}}\right\}\\ +\Lambda _{t+j}^{3}\left\{\frac{N_{t+j}}{P_{t+j}}+\frac{W_{t+j}h_{t+j}}{P_{t+j}}+\int _{0}^{1}\frac{F_{t+j}\!\left(i\right)}{P_{t+j}}s_{t+j}\!\left(i\right)di+\frac{r_{t+j}^{D}D_{t+j}}{P_{t+j}}\right.\\\qquad\qquad\left.-C_{t+j}-\frac{r_{t+j}^{L}L_{t+j}}{P_{t+j}}-\frac{r_{t+j}^{CC}CC_{t+j}}{P_{t+j}}-\frac{M_{t+j}}{P_{t+j}}\right\} \end{array}\right]. \end{equation}
The first-order conditions for the representative household’s problem are as follows:
(a) First-order conditions with respect to
 $B_{t}$
:(A.6)
$B_{t}$
:(A.6) \begin{equation} \frac{\Lambda _{t}^{1}}{r_{t}}=\beta \frac{\mathrm{\mathbb{E}}_{t}\left(\Lambda _{t+1}^{1}\right)P_{t}}{P_{t+1}}. \end{equation}
\begin{equation} \frac{\Lambda _{t}^{1}}{r_{t}}=\beta \frac{\mathrm{\mathbb{E}}_{t}\left(\Lambda _{t+1}^{1}\right)P_{t}}{P_{t+1}}. \end{equation}
(b) First-order conditions with respect to
 $s_{t}$
for all
$s_{t}$
for all
 $i$
:(A.7)
$i$
:(A.7) \begin{equation} \Lambda _{t}^{1}\frac{Q_{t}\!\left(i\right)}{P_{t}}=\Lambda _{t}^{3}\frac{F_{t}\!\left(i\right)}{P_{t}}+\beta \mathrm{\mathbb{E}}_{t}\left[\frac{\Lambda _{t+1}^{1}Q_{t+1}\!\left(i\right)}{P_{t+1}}\right]. \end{equation}
\begin{equation} \Lambda _{t}^{1}\frac{Q_{t}\!\left(i\right)}{P_{t}}=\Lambda _{t}^{3}\frac{F_{t}\!\left(i\right)}{P_{t}}+\beta \mathrm{\mathbb{E}}_{t}\left[\frac{\Lambda _{t+1}^{1}Q_{t+1}\!\left(i\right)}{P_{t+1}}\right]. \end{equation}
(c) First-order conditions with respect to
 $N_{t}$
:(A.8)
$N_{t}$
:(A.8) \begin{equation} \Lambda _{t}^{1}-\Lambda _{^{t}}^{3}=\Lambda _{t}^{2}\left[\frac{M_{t}^{A}}{P_{t}}\right]^{1/\omega }\nu ^{1/\omega }\left[\frac{N_{t}}{P_{t}}\right]^{-1/\omega }. \end{equation}
\begin{equation} \Lambda _{t}^{1}-\Lambda _{^{t}}^{3}=\Lambda _{t}^{2}\left[\frac{M_{t}^{A}}{P_{t}}\right]^{1/\omega }\nu ^{1/\omega }\left[\frac{N_{t}}{P_{t}}\right]^{-1/\omega }. \end{equation}
(d) First-order conditions with respect to
 $D_{t}$
:(A.9)
$D_{t}$
:(A.9) \begin{equation} \Lambda _{t}^{1}-r_{t}^{D}\Lambda _{^{t}}^{3}=\Lambda _{t}^{2}\left[\frac{M_{t}^{A}}{P_{t}}\right]^{1/\omega }\xi ^{1/\omega }\left[\frac{D_{t}}{P_{t}}\right]^{-1/\omega }.\end{equation}
\begin{equation} \Lambda _{t}^{1}-r_{t}^{D}\Lambda _{^{t}}^{3}=\Lambda _{t}^{2}\left[\frac{M_{t}^{A}}{P_{t}}\right]^{1/\omega }\xi ^{1/\omega }\left[\frac{D_{t}}{P_{t}}\right]^{-1/\omega }.\end{equation}
(e) First-order conditions with respect to
 $CC_{t}$
: (A.10)
$CC_{t}$
: (A.10) \begin{equation} -\Lambda _{t}^{1}+r_{t}^{CC}\Lambda _{^{t}}^{3}=\Lambda _{t}^{2}\left[\frac{M_{t}^{A}}{P_{t}}\right]^{1/\omega }\left(1-\nu -\xi \right)^{1/\omega }\left[\frac{CC_{t}}{P_{t}}\right]^{-1/\omega }\end{equation}
\begin{equation} -\Lambda _{t}^{1}+r_{t}^{CC}\Lambda _{^{t}}^{3}=\Lambda _{t}^{2}\left[\frac{M_{t}^{A}}{P_{t}}\right]^{1/\omega }\left(1-\nu -\xi \right)^{1/\omega }\left[\frac{CC_{t}}{P_{t}}\right]^{-1/\omega }\end{equation}
(f) First-order conditions with respect to
 $L_{t}$
, (A.11)
$L_{t}$
, (A.11) \begin{equation} \Lambda _{t}^{1}=r_{t}^{L}\Lambda _{t}^{3}.\end{equation}
\begin{equation} \Lambda _{t}^{1}=r_{t}^{L}\Lambda _{t}^{3}.\end{equation}
(g) First-order conditions with respect to
 $h_{t}$
, (A.12)
$h_{t}$
, (A.12) \begin{equation} \eta a_{t}=\Lambda _{t}^{3}\frac{W_{t}}{P_{t}}.\end{equation}
\begin{equation} \eta a_{t}=\Lambda _{t}^{3}\frac{W_{t}}{P_{t}}.\end{equation}
(h) First-order conditions with respect to
 $C_{t}$
:(A.13)
$C_{t}$
:(A.13) \begin{equation} \frac{a_{t}}{C_{t}}\left[1-\eta\!\left(\frac{v_{t}P_{t}C_{t}}{M_{t}^{\,A}}\right)^{\chi }\right]=\Lambda _{t}^{3}.\end{equation}
\begin{equation} \frac{a_{t}}{C_{t}}\left[1-\eta\!\left(\frac{v_{t}P_{t}C_{t}}{M_{t}^{\,A}}\right)^{\chi }\right]=\Lambda _{t}^{3}.\end{equation}
(i) First-order conditions with respect to
 $M_{t}^{A}$
:(A.14)
$M_{t}^{A}$
:(A.14) \begin{equation} \eta a_{t}\left(\frac{v_{t}P_{t}C_{t}}{M_{t}^{\,A}}\right)^{\chi }=\left(\frac{M_{t}^{\,A}}{P_{t}}\right)\Lambda _{t}^{2}.\end{equation}
\begin{equation} \eta a_{t}\left(\frac{v_{t}P_{t}C_{t}}{M_{t}^{\,A}}\right)^{\chi }=\left(\frac{M_{t}^{\,A}}{P_{t}}\right)\Lambda _{t}^{2}.\end{equation}
(j) First-order conditions with respect to
 $M_{t}$
,(A.15)
$M_{t}$
,(A.15) \begin{equation} \Lambda _{t}^{3}=\beta \mathrm{\mathbb{E}}_{t}\left[\frac{\Lambda _{t+1}^{1}P_{t}}{P_{t+1}}\right]. \end{equation}
\begin{equation} \Lambda _{t}^{3}=\beta \mathrm{\mathbb{E}}_{t}\left[\frac{\Lambda _{t+1}^{1}P_{t}}{P_{t+1}}\right]. \end{equation}
A.2. Intermediate Goods-producing Firm optimization
Following Belongia and Ireland (Reference Belongia and Ireland2014), the representative intermediate goods-producing firm’s total, real market value is proportional to
where
To maximize total market value, we substitute equation (B.2) into (B.1). The first-order condition with respect to
![]() $P_{t}(i)$
becomes
$P_{t}(i)$
becomes
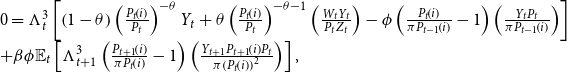 \begin{equation} \begin{array}{l} 0=\Lambda _{t}^{3}\left[\left(1-\theta \right)\left(\frac{P_{t}\!\left(i\right)}{P_{t}}\right)^{-\theta }Y_{t}+\theta \left(\frac{P_{t}\!\left(i\right)}{P_{t}}\right)^{-\theta -1}\left(\frac{W_{t}Y_{t}}{P_{t}Z_{t}}\right)-\phi \left(\frac{P_{t}\!\left(i\right)}{\pi P_{t-1}\!\left(i\right)}-1\right)\left(\frac{Y_{t}P_{t}}{\pi P_{t-1}\!\left(i\right)}\right)\right]\\ +\beta \phi \mathrm{\mathbb{E}}_{t}\left[\Lambda _{t+1}^{3}\left(\frac{P_{t+1}\!\left(i\right)}{\pi P_{t}\!\left(i\right)}-1\right)\left(\frac{Y_{t+1}P_{t+1}\!\left(i\right)P_{t}}{\pi \left(P_{t}\!\left(i\right)\right)^{2}}\right)\right], \end{array} \end{equation}
\begin{equation} \begin{array}{l} 0=\Lambda _{t}^{3}\left[\left(1-\theta \right)\left(\frac{P_{t}\!\left(i\right)}{P_{t}}\right)^{-\theta }Y_{t}+\theta \left(\frac{P_{t}\!\left(i\right)}{P_{t}}\right)^{-\theta -1}\left(\frac{W_{t}Y_{t}}{P_{t}Z_{t}}\right)-\phi \left(\frac{P_{t}\!\left(i\right)}{\pi P_{t-1}\!\left(i\right)}-1\right)\left(\frac{Y_{t}P_{t}}{\pi P_{t-1}\!\left(i\right)}\right)\right]\\ +\beta \phi \mathrm{\mathbb{E}}_{t}\left[\Lambda _{t+1}^{3}\left(\frac{P_{t+1}\!\left(i\right)}{\pi P_{t}\!\left(i\right)}-1\right)\left(\frac{Y_{t+1}P_{t+1}\!\left(i\right)P_{t}}{\pi \left(P_{t}\!\left(i\right)\right)^{2}}\right)\right], \end{array} \end{equation}
for all
![]() $t=0,1,2\ldots$
.
$t=0,1,2\ldots$
.
A.3. Efficient Allocation for Social planner
In accordance with their definitions,
![]() $Y_{t}^{*}, P_{t}^{*}$
, and
$Y_{t}^{*}, P_{t}^{*}$
, and
![]() $h_{t}^{*}$
are expressed by:
$h_{t}^{*}$
are expressed by:
 \begin{equation} Y_{t}^{*}=\left[\int _{0}^{1}Y_{t}^{*}\!\left(i\right)^{\frac{\theta -1}{\theta }}di\right]^{\frac{\theta }{\theta -1}}, \end{equation}
\begin{equation} Y_{t}^{*}=\left[\int _{0}^{1}Y_{t}^{*}\!\left(i\right)^{\frac{\theta -1}{\theta }}di\right]^{\frac{\theta }{\theta -1}}, \end{equation}
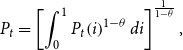 \begin{equation} P_{t}=\left[\int _{0}^{1}P_{t}\!\left(i\right)^{1-\theta }di\right]^{\frac{1}{1-\theta }}, \end{equation}
\begin{equation} P_{t}=\left[\int _{0}^{1}P_{t}\!\left(i\right)^{1-\theta }di\right]^{\frac{1}{1-\theta }}, \end{equation}
The optimization problem of the social planner is given by:
subject to
 \begin{equation} Z_{t}\left(\int _{0}^{1}h_{t}^{*}\!\left(i\right)^{\frac{\theta -1}{\theta }}di\right)^{\frac{\theta }{\theta -1}}=Y_{t}^{*}. \end{equation}
\begin{equation} Z_{t}\left(\int _{0}^{1}h_{t}^{*}\!\left(i\right)^{\frac{\theta -1}{\theta }}di\right)^{\frac{\theta }{\theta -1}}=Y_{t}^{*}. \end{equation}
The Lagrangian expression is
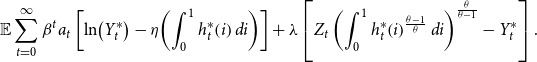 \begin{equation} \mathrm{\mathbb{E}}\sum _{t=0}^{\infty }\beta ^{t}a_{t}\left[\ln\!\left(Y_{t}^{*}\right)-\eta\!\left(\int _{0}^{1}h_{t}^{*}\!\left(i\right)di\right)\right]+\lambda \left[Z_{t}\left(\int _{0}^{1}h_{t}^{*}\!\left(i\right)^{\frac{\theta -1}{\theta }}di\right)^{\frac{\theta }{\theta -1}}-Y_{t}^{*}\right]. \end{equation}
\begin{equation} \mathrm{\mathbb{E}}\sum _{t=0}^{\infty }\beta ^{t}a_{t}\left[\ln\!\left(Y_{t}^{*}\right)-\eta\!\left(\int _{0}^{1}h_{t}^{*}\!\left(i\right)di\right)\right]+\lambda \left[Z_{t}\left(\int _{0}^{1}h_{t}^{*}\!\left(i\right)^{\frac{\theta -1}{\theta }}di\right)^{\frac{\theta }{\theta -1}}-Y_{t}^{*}\right]. \end{equation}
The first-order conditions of
![]() $Y_{t}^{*}$
and
$Y_{t}^{*}$
and
![]() $h_{t}^{*}(i)$
are given by:
$h_{t}^{*}(i)$
are given by:
(a) First-order conditions with respect to
 $Y_{t}^{*}$
are(A.25)
$Y_{t}^{*}$
are(A.25) \begin{equation} \frac{\beta ^{t}a_{t}}{Y_{t}^{*}}=\lambda . \end{equation}
\begin{equation} \frac{\beta ^{t}a_{t}}{Y_{t}^{*}}=\lambda . \end{equation}
(b) First-order conditions with respect to
 $h_{t}^{*}(i)$
combined with the equation (A.25) are(A.26)
$h_{t}^{*}(i)$
combined with the equation (A.25) are(A.26) \begin{equation} \eta =\frac{Z_{t}}{Y_{t}^{*}}\left[\int _{0}^{1}h_{t}^{*}\!\left(i\right)^{\frac{\theta -1}{\theta }}di\right]^{\frac{1}{\theta -1}}h_{t}^{*}\!\left(i\right)^{\frac{-1}{\theta }}. \end{equation}
\begin{equation} \eta =\frac{Z_{t}}{Y_{t}^{*}}\left[\int _{0}^{1}h_{t}^{*}\!\left(i\right)^{\frac{\theta -1}{\theta }}di\right]^{\frac{1}{\theta -1}}h_{t}^{*}\!\left(i\right)^{\frac{-1}{\theta }}. \end{equation}
Substituting the equation (A.22) into the equation (A.26), we get
(A.27)which can be re-expressed by: \begin{equation} h_{t}^{*}\!\left(i\right)^{\frac{-1}{\theta }}=\eta \left[\int _{0}^{1}h_{t}^{*}\!\left(i\right)^{\frac{\theta -1}{\theta }}di\right], \end{equation}
(A.28)
\begin{equation} h_{t}^{*}\!\left(i\right)^{\frac{-1}{\theta }}=\eta \left[\int _{0}^{1}h_{t}^{*}\!\left(i\right)^{\frac{\theta -1}{\theta }}di\right], \end{equation}
(A.28) \begin{equation} h_{t}^{*}\!\left(i\right)^{\frac{-1}{\theta }}=\eta h_{t}^{*}\!\left(i\right)^{\frac{\theta -1}{\theta }}.\end{equation}
\begin{equation} h_{t}^{*}\!\left(i\right)^{\frac{-1}{\theta }}=\eta h_{t}^{*}\!\left(i\right)^{\frac{\theta -1}{\theta }}.\end{equation}
Then, we can get the relationship:
and finally if we substitute (A.29) into the relationship,
![]() $Y_{t}^{*}=Z_{t}h_{t}^{*}$
, the expression
$Y_{t}^{*}=Z_{t}h_{t}^{*}$
, the expression
is acquired.
A.4. Systematic Equilibrium
Under the systematic equilibrium environment, all intermediate goods-producing firms make the same decision, so we can set
![]() $Y_{t}(i)=Y_{t}, h_{t}(i)=h_{t}, P_{t}(i)=P_{t}, F_{t}(i)=F_{t}$
, and
$Y_{t}(i)=Y_{t}, h_{t}(i)=h_{t}, P_{t}(i)=P_{t}, F_{t}(i)=F_{t}$
, and
![]() $Q_{t}(i)=Q_{t}$
for all
$Q_{t}(i)=Q_{t}$
for all
![]() $i\in [0,1]$
and
$i\in [0,1]$
and
![]() $t=0,1,2,\ldots$
. For the market clearing condition, we set
$t=0,1,2,\ldots$
. For the market clearing condition, we set
![]() $M_{t}=M_{t-1}+Tr_{t}, B_{t}=B_{t-1}=0$
, and
$M_{t}=M_{t-1}+Tr_{t}, B_{t}=B_{t-1}=0$
, and
![]() $s_{t}(i)=s_{t-1}(i)=1$
for all
$s_{t}(i)=s_{t-1}(i)=1$
for all
![]() $i\in [0,1]$
and
$i\in [0,1]$
and
![]() $t=0,1,2,\ldots$
. Collecting equations with the conditions mentioned above, we have 46 variables and 46 system equations for equilibrium.
$t=0,1,2,\ldots$
. Collecting equations with the conditions mentioned above, we have 46 variables and 46 system equations for equilibrium.
B. Stationary system
B.1. The Stationary system
Since the real variables in the system inherits a unit root process from the technology shock, and the nominal variables also hold a unit root process from the implementation of monetary policy represented by the Taylor rule, the variables in this system will be non-stationary. Therefore, we need to convert the system to be stationary along the model’s balanced growth path. By redefining the variables, we can obtain a new stationary system.
A. 11 Real variables:
 $c_{t}=C_{t}/Z_{t-1}, y_{t}=Y_{t}/Z_{t-1}, y_{t}^{*}=Y_{t}^{*}/Z_{t-1}, g_{t}^{y}, g_{t}^{*}, h_{t}, h_{t}^{s}, f_{t}=F_{t}/(P_{t} Z_{t-1}), \lambda _{t}^{1}=Z_{t-1}\Lambda _{t}^{1}, \lambda _{t}^{2}=Z_{t-1}\Lambda _{t}^{2}, \lambda _{t}^{3}=Z_{t-1}\Lambda _{t}^{3}$
.
$c_{t}=C_{t}/Z_{t-1}, y_{t}=Y_{t}/Z_{t-1}, y_{t}^{*}=Y_{t}^{*}/Z_{t-1}, g_{t}^{y}, g_{t}^{*}, h_{t}, h_{t}^{s}, f_{t}=F_{t}/(P_{t} Z_{t-1}), \lambda _{t}^{1}=Z_{t-1}\Lambda _{t}^{1}, \lambda _{t}^{2}=Z_{t-1}\Lambda _{t}^{2}, \lambda _{t}^{3}=Z_{t-1}\Lambda _{t}^{3}$
.B. 9 Money stock variables:
 $m_{t}^{A}=M_{t}^{A}/(P_{t}Z_{t-1}), n_{t}=N_{t}/(P_{t}Z_{t-1}), d_{t}=D_{t}/(P_{t}Z_{t-1}), cc_{t}=CC_{t}/(P_{t}Z_{t-1}), m_{t}=M_{t}/(P_{t}Z_{t-1}), l_{t}=L_{t}/(P_{t}Z_{t-1}), n_{t}^{v}=N_{t}^{v}/(P_{t}Z_{t-1}), m_{t}^{S}=M_{t}^{S}/(P_{t}Z_{t-1}), e_{t}=E_{t}/(P_{t}Z_{t-1})$
.
$m_{t}^{A}=M_{t}^{A}/(P_{t}Z_{t-1}), n_{t}=N_{t}/(P_{t}Z_{t-1}), d_{t}=D_{t}/(P_{t}Z_{t-1}), cc_{t}=CC_{t}/(P_{t}Z_{t-1}), m_{t}=M_{t}/(P_{t}Z_{t-1}), l_{t}=L_{t}/(P_{t}Z_{t-1}), n_{t}^{v}=N_{t}^{v}/(P_{t}Z_{t-1}), m_{t}^{S}=M_{t}^{S}/(P_{t}Z_{t-1}), e_{t}=E_{t}/(P_{t}Z_{t-1})$
.C. 4 Money growth variables:
 $\mu _{t}^{N}, \mu _{t}^{D}, \mu _{t}^{CC}, \mu _{t}^{Q}$
.
$\mu _{t}^{N}, \mu _{t}^{D}, \mu _{t}^{CC}, \mu _{t}^{Q}$
.D. 3 Price variables:
 $\pi _{t}=P_{t}/P_{t-1}, w_{t}=W_{t}/(P_{t}Z_{t-1}), q_{t}=Q_{t}/(P_{r}Z_{t-1})$
.
$\pi _{t}=P_{t}/P_{t-1}, w_{t}=W_{t}/(P_{t}Z_{t-1}), q_{t}=Q_{t}/(P_{r}Z_{t-1})$
.E. 5 Interest rates:
 $r_{t}, r_{t}^{D}, r_{t}^{L}, r_{t}^{CC}, r_{t}^{A}$
.
$r_{t}, r_{t}^{D}, r_{t}^{L}, r_{t}^{CC}, r_{t}^{A}$
.F. 8 User costs, expenditure shares, and price dual variables:
 $u_{t}^{A}, u_{t}^{N}, u_{t}^{D}, u_{t}^{CC}, s_{t}^{N}, s_{t}^{D}, s_{t}^{CC}, \pi _{t}^{P}$
.
$u_{t}^{A}, u_{t}^{N}, u_{t}^{D}, u_{t}^{CC}, s_{t}^{N}, s_{t}^{D}, s_{t}^{CC}, \pi _{t}^{P}$
.G. 6 Shocks:
 $v_{t}, a_{t}, z_{t}=Z_{t}/Z_{t-1}, \tau _{t}, \varpi _{t}, x_{t}$
.
$v_{t}, a_{t}, z_{t}=Z_{t}/Z_{t-1}, \tau _{t}, \varpi _{t}, x_{t}$
.
B.2. The Stationary Equilibrium
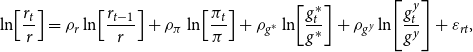 \begin{equation}\ln\!\left[\frac{r_{t}}{r}\right]=\rho _{r}\ln\!\left[\frac{r_{t-1}}{r}\right]+\rho _{\pi }\ln\!\left[\frac{\pi _{t}}{\pi }\right]+\rho _{{g^{*}}}\ln\!\left[\frac{g_{t}^{*}}{g^{*}}\right]+\rho _{{g^{y}}}\ln\!\left[\frac{g_{t}^{y}}{g^{y}}\right]+\varepsilon _{rt},\end{equation}
\begin{equation}\ln\!\left[\frac{r_{t}}{r}\right]=\rho _{r}\ln\!\left[\frac{r_{t-1}}{r}\right]+\rho _{\pi }\ln\!\left[\frac{\pi _{t}}{\pi }\right]+\rho _{{g^{*}}}\ln\!\left[\frac{g_{t}^{*}}{g^{*}}\right]+\rho _{{g^{y}}}\ln\!\left[\frac{g_{t}^{y}}{g^{y}}\right]+\varepsilon _{rt},\end{equation}
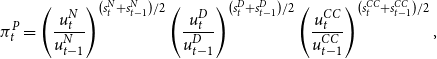 \begin{equation}\pi _{t}^{P}=\left(\frac{u_{t}^{N}}{u_{t-1}^{N}}\right)^{\left(s_{t}^{N}+s_{t-1}^{N}\right)/2}\left(\frac{u_{t}^{D}}{u_{t-1}^{D}}\right)^{\left(s_{t}^{D}+s_{t-1}^{D}\right)/2}\left(\frac{u_{t}^{CC}}{u_{t-1}^{CC}}\right)^{\left(s_{t}^{CC}+s_{t-1}^{CC}\right)/2},\end{equation}
\begin{equation}\pi _{t}^{P}=\left(\frac{u_{t}^{N}}{u_{t-1}^{N}}\right)^{\left(s_{t}^{N}+s_{t-1}^{N}\right)/2}\left(\frac{u_{t}^{D}}{u_{t-1}^{D}}\right)^{\left(s_{t}^{D}+s_{t-1}^{D}\right)/2}\left(\frac{u_{t}^{CC}}{u_{t-1}^{CC}}\right)^{\left(s_{t}^{CC}+s_{t-1}^{CC}\right)/2},\end{equation}
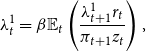 \begin{equation}\lambda _{t}^{1}=\beta \mathrm{\mathbb{E}}_{t}\left(\frac{\lambda _{t+1}^{1}r_{t}}{\pi _{t+1}z_{t}}\right),\end{equation}
\begin{equation}\lambda _{t}^{1}=\beta \mathrm{\mathbb{E}}_{t}\left(\frac{\lambda _{t+1}^{1}r_{t}}{\pi _{t+1}z_{t}}\right),\end{equation}
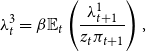 \begin{equation}\lambda _{t}^{3}=\beta \mathrm{\mathbb{E}}_{t}\left(\frac{\lambda _{t+1}^{1}}{z_{t}\pi _{t+1}}\right),\end{equation}
\begin{equation}\lambda _{t}^{3}=\beta \mathrm{\mathbb{E}}_{t}\left(\frac{\lambda _{t+1}^{1}}{z_{t}\pi _{t+1}}\right),\end{equation}
C. Parameter calibration
C.1. Section 3.1.1
The parameters which characterize the general New Keynesian framework from chapter 2 are unchanged (
![]() $\beta, \eta, \chi, \theta, \phi$
, and
$\beta, \eta, \chi, \theta, \phi$
, and
![]() $\omega$
).
$\omega$
).
The setting
![]() $\pi$
= 1.005 is still valid in this period. The value
$\pi$
= 1.005 is still valid in this period. The value
![]() $z$
= 1.00445 supports 1.79% of the annual growth of real variables in the model. The value
$z$
= 1.00445 supports 1.79% of the annual growth of real variables in the model. The value
![]() $\sigma _{z}$
= 0.01497 is calculated from the standard deviation of real, per capita growth in the U.S. data within the data period. The value of
$\sigma _{z}$
= 0.01497 is calculated from the standard deviation of real, per capita growth in the U.S. data within the data period. The value of
![]() $v$
= 0.2646 makes the steady-state ratio of the sum of monetary service provision to nominal consumption expenditures in the model equal to 2.74. This setting is comparable with the U.S. data, which equals 2.732 from 2006 to 2018. The setting
$v$
= 0.2646 makes the steady-state ratio of the sum of monetary service provision to nominal consumption expenditures in the model equal to 2.74. This setting is comparable with the U.S. data, which equals 2.732 from 2006 to 2018. The setting
![]() $\sigma _{v}$
= 0.2995 can be obtained from the standard deviation of the ratio of the monetary services provision to nominal consumption expenditures in the U.S. data within the limited period. For the composition of monetary service provider component, the settings
$\sigma _{v}$
= 0.2995 can be obtained from the standard deviation of the ratio of the monetary services provision to nominal consumption expenditures in the U.S. data within the limited period. For the composition of monetary service provider component, the settings
![]() $\nu$
= 0.15 and
$\nu$
= 0.15 and
![]() $\xi$
= 0.60 induce the steady-state ratio of currency, deposit, and credit cards transaction to be 10.8, 87.2, 2.0, which are consistent with the ratios given by the CFS data.
$\xi$
= 0.60 induce the steady-state ratio of currency, deposit, and credit cards transaction to be 10.8, 87.2, 2.0, which are consistent with the ratios given by the CFS data.
The most noticeable changes can be tracked from
![]() $\tau$
= 0.1493, which explains the average ratio of total reserves to the deposit component from 2006 to 2019. The Federal Reserve began paying interest on reserves held by the banks in 2008. Since then, the reserve ratio has drastically surged, reaching 27.4% in August 2014. The value
$\tau$
= 0.1493, which explains the average ratio of total reserves to the deposit component from 2006 to 2019. The Federal Reserve began paying interest on reserves held by the banks in 2008. Since then, the reserve ratio has drastically surged, reaching 27.4% in August 2014. The value
![]() $\sigma _{\tau }$
= 0.08 reflects the standard deviation of the reserve ratio within the data period. The setting
$\sigma _{\tau }$
= 0.08 reflects the standard deviation of the reserve ratio within the data period. The setting
![]() $x$
= 0.0115 implies that 2.63% of the steady-state total aggregate output can be explained by banking activity, because the deposit costs are measured in the units of the finished good. In the same data period, Federal Reserve and BEA data display 2.64% and 2.63%, respectively. The value
$x$
= 0.0115 implies that 2.63% of the steady-state total aggregate output can be explained by banking activity, because the deposit costs are measured in the units of the finished good. In the same data period, Federal Reserve and BEA data display 2.64% and 2.63%, respectively. The value
![]() $\sigma _{x}$
= 0.00115 explains the standard deviation of banking activities normalized by the output within the data period. The setting
$\sigma _{x}$
= 0.00115 explains the standard deviation of banking activities normalized by the output within the data period. The setting
![]() $\varpi$
= 0.0228 remains the same, because the calibration shares the same data period. However, the empirical data show the standard deviation
$\varpi$
= 0.0228 remains the same, because the calibration shares the same data period. However, the empirical data show the standard deviation
![]() $\sigma _{\varpi }$
= 0.0018, which can be calculated from the empirical data.
$\sigma _{\varpi }$
= 0.0018, which can be calculated from the empirical data.
We assume the value of the persistence parameters,
![]() $\rho _{v}, \rho _{\tau }, \rho _{x}$
, and
$\rho _{v}, \rho _{\tau }, \rho _{x}$
, and
![]() $\rho _{\varpi }$
, still remain the same. For the monetary policy, equation (28), the parameters are calculated by the regressions using the federal funds rate, lagged federal funds rate, and inflation rate. The results report
$\rho _{\varpi }$
, still remain the same. For the monetary policy, equation (28), the parameters are calculated by the regressions using the federal funds rate, lagged federal funds rate, and inflation rate. The results report
![]() $\rho _{r}$
= 1.005,
$\rho _{r}$
= 1.005,
![]() $\rho _{\pi }$
= 0.2226, and the standard deviation,
$\rho _{\pi }$
= 0.2226, and the standard deviation,
![]() $\sigma _{r}$
= 0.4752.
$\sigma _{r}$
= 0.4752.













