Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T07:24:12.805Z Has data issue: false hasContentIssue false
  • English
  • Français

Wieferich pairs and Barker sequences, II

Part of: Communication, information Combinatorics Designs and configurations Elementary number theory

Published online by Cambridge University Press:  01 April 2014

Peter Borwein  and
Michael J. Mossinghoff
Peter Borwein
Affiliation:
Department of Mathematics, Simon Fraser University, Burnaby, BC V5A 1S6, Canada email [email protected]
Michael J. Mossinghoff
Affiliation:
Department of Mathematics, Davidson College, Davidson, NC 28035-6996, USA email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

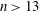We show that if a Barker sequence of length $n>13$ exists, then either n $=$ 3 979 201 339 721 749 133 016 171 583 224 100, or 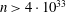$n > 4\cdot 10^{33}$. This improves the lower bound on the length of a long Barker sequence by a factor of nearly 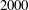$2000$. We also obtain eighteen additional integers 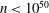$n<10^{50}$ that cannot be ruled out as the length of a Barker sequence, and find more than 237 000 additional candidates 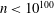$n<10^{100}$. These results are obtained by completing extensive searches for Wieferich prime pairs and using them, together with a number of arithmetic restrictions on $n$, to construct qualifying integers below a given bound. We also report on some updated computations regarding open cases of the circulant Hadamard matrix problem.

MSC classification

Secondary: 05B20: Matrices (incidence, Hadamard, etc.) 94A55: Shift register sequences and sequences over finite alphabets 05-04: Explicit machine computation and programs (not the theory of computation or programming) 05B10: Difference sets (number-theoretic, group-theoretic, etc.) 11A07: Congruences; primitive roots; residue systems
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Issue 1 , 2014 , pp. 24 - 32
Copyright
© The Author(s) 2014 

References

Eliahou, S. and Kervaire, M., ‘Barker sequences and difference sets’, Enseign. Math. (2) 38 (1992) no. 3–4, 345–382; Corrigendum, Enseign. Math. (2) 40 (1994) no. 1–2, 109–111; MR 1189012 (93i:11018).Google Scholar
Eliahou, S., Kervaire, M. and Saffari, B., ‘A new restriction on the lengths of Golay complementary sequences’, J. Combin. Theory Ser. A 55 (1990) no. 1, 49–59; MR 1070014 (91i:11020).Google Scholar
Jedwab, J. and Lloyd, S., ‘A note on the nonexistence of Barker sequences’, Des. Codes Cryptogr. 2 (1992) no. 1, 93–97; MR 1157481 (93e:11032).Google Scholar
Leung, K. H. and Schmidt, B., ‘The field descent method’, Des. Codes Cryptogr. 36 (2005) no. 2, 171–188; MR 2211106 (2007g:05023).Google Scholar
Leung, K. H. and Schmidt, B., ‘New restrictions on possible orders of circulant Hadamard matrices’, Des. Codes Cryptogr. 64 (2012) no. 1–2, 143–151; MR 2914407.Google Scholar
Mossinghoff, M. J., ‘Wieferich pairs and Barker sequences’, Des. Codes Cryptogr. 53 (2009) no. 3, 149–163; MR 2545689 (2011c:11039).Google Scholar
Mossinghoff, M. J., ‘Wieferich prime pairs, Barker sequences, and circulant Hadamard matrices’, 2013, http://www.cecm.sfu.ca/∼mjm/WieferichBarker.Google Scholar
Schmidt, B., ‘Cyclotomic integers and finite geometry’, J. Amer. Math. Soc. 12 (1999) no. 4, 929–952; MR 1671453 (2000a:05042).Google Scholar
Tarjan, R., ‘Enumeration of the elementary circuits of a directed graph’, SIAM J. Comput. 2 (1973) 211–216; MR 0325448 (48 #3795).Google Scholar
Turyn, R., ‘Character sums and difference sets’, Pacific J. Math. 15 (1965) 319–346; MR 0179098 (31 #3349).Google Scholar
Turyn, R. and Storer, J., ‘On binary sequences’, Proc. Amer. Math. Soc. 12 (1961) 394–399; MR 0125026 (23 #A2333).CrossRefGoogle Scholar