Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T21:44:13.866Z Has data issue: false hasContentIssue false
  • English
  • Français

Rational functions with maximal radius of absolute monotonicity

Part of: Optimality conditions Numerical analysis: Ordinary differential equations Approximations and expansions Algorithms - Computer Science

Published online by Cambridge University Press:  01 May 2014

Lajos Lóczi  and
David I. Ketcheson
Lajos Lóczi
Affiliation:
Computer, Electrical and Mathematical Sciences and Engineering, King Abdullah University of Science and Technology (KAUST), 4700 KAUST, Thuwal, 23955, Saudi Arabia email [email protected]
David I. Ketcheson
Affiliation:
Computer, Electrical and Mathematical Sciences and Engineering, King Abdullah University of Science and Technology (KAUST), 4700 KAUST, Thuwal, 23955, Saudi Arabia email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the radius of absolute monotonicity 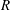$R$ of rational functions with numerator and denominator of degree $s$ that approximate the exponential function to order 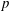$p$. Such functions arise in the application of implicit $s$-stage, order 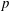$p$ Runge–Kutta methods for initial value problems, and the radius of absolute monotonicity governs the numerical preservation of properties like positivity and maximum-norm contractivity. We construct a function with 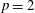$p=2$ and 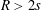$R>2s$, disproving a conjecture of van de Griend and Kraaijevanger. We determine the maximum attainable radius for functions in several one-parameter families of rational functions. Moreover, we prove earlier conjectured optimal radii in some families with two or three parameters via uniqueness arguments for systems of polynomial inequalities. Our results also prove the optimality of some strong stability preserving implicit and singly diagonally implicit Runge–Kutta methods. Whereas previous results in this area were primarily numerical, we give all constants as exact algebraic numbers.

MSC classification

Secondary: 65L06: Multistep, Runge-Kutta and extrapolation methods 68W30: Symbolic computation and algebraic computation 41A20: Approximation by rational functions 49K30: Optimal solutions belonging to restricted classes
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Issue 1 , 2014 , pp. 159 - 205
Copyright
© The Author(s) 2014 

References

Bolley, C. and Crouzeix, M., ‘Conservation de la positivité lors de la discrétisation des problémes d’évolution paraboliques’, RAIRO Anal. Numér. 12 (1978) 237–245.Google Scholar
Butcher, J. C., Numerical methods for ordinary differential equations , 2nd edn (Wiley, 2008).Google Scholar
Ferracina, L. and Spijker, M. N., ‘Strong stability of singly-diagonally-implicit Runge–Kutta methods’, Appl. Numer. Math. 58 (2008) 1675–1686.Google Scholar
Gottlieb, S., Ketcheson, D. I. and Shu, C.-W., Strong stability preserving Runge–Kutta and multistep time discretizations (World Scientific, 2011).Google Scholar
van de Griend, J. A. and Kraaijevanger, J. F. B. M., ‘Absolute monotonicity of rational functions occurring in the numerical solution of initial value problems’, Numer. Math. 49 (1986) 413–424.Google Scholar
Hairer, E. and Wanner, G., Solving ordinary differential equations II: stiff and differential-algebraic problems (Springer, 1991).Google Scholar
Ketcheson, D. I., ‘Computation of optimal monotonicity preserving general linear methods’, Math. Comp. 78 (2009) 1497–1513.Google Scholar
Ketcheson, D. I., ‘High order strong stability preserving time integrators and numerical wave propagation methods for hyperbolic PDEs’, PhD Thesis, University of Washington, 2009.Google Scholar
Ketcheson, D. I., Macdonald, C. B. and Gottlieb, S., ‘Optimal implicit strong stability preserving Runge–Kutta methods’, Appl. Numer. Math. 59 (2009) 373–392.Google Scholar
Kraaijevanger, J. F. B. M., ‘Absolute monotonicity of polynomials occurring in the numerical solution of initial value problems’, Numer. Math. 48 (1986) 303–322.Google Scholar
Kraaijevanger, J. F. B. M., ‘Contractivity of Runge–Kutta Methods’, BIT 31 (1991) 482–528.Google Scholar
Spijker, M. N., ‘Contractivity in the numerical solution of initial value problems’, Numer. Math. 42 (1983) 271–290.Google Scholar