Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T13:12:01.324Z Has data issue: false hasContentIssue false
  • English
  • Français

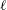On the quaternion $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\ell $-isogeny path problem

Published online by Cambridge University Press:  01 August 2014

David Kohel ,
Kristin Lauter ,
Christophe Petit  and
Jean-Pierre Tignol
David Kohel
Affiliation:
Institut de Mathématiques de Marseille, Université d’Aix-Marseille, 163, avenue de Luminy, Case 907, 13288 Marseille Cedex 9, France email [email protected]
Kristin Lauter
Affiliation:
Microsoft Research, One Microsoft Way, Redmond, WA 98052, USA email [email protected]
Christophe Petit
Affiliation:
UCL Crypto Group, Université catholique de Louvain, Place du Levant 3, B1348 Louvain-la-Neuve, Belgium email [email protected]
Jean-Pierre Tignol
Affiliation:
UCL – ICTEAM/INMA, Université catholique de Louvain, Avenue G. Lemaitre 4, box L4.05.01, B1348 Louvain-la-Neuve, Belgium email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

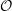Let $\mathcal{O}$ be a maximal order in a definite quaternion algebra over 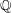$\mathbb{Q}$ of prime discriminant $p$, and 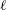$\ell $ a small prime. We describe a probabilistic algorithm which, for a given left 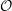$\mathcal{O}$-ideal, computes a representative in its left ideal class of 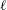$\ell $-power norm. In practice the algorithm is efficient and, subject to heuristics on expected distributions of primes, runs in expected polynomial time. This solves the underlying problem for a quaternion analog of the Charles–Goren–Lauter hash function, and has security implications for the original CGL construction in terms of supersingular elliptic curves.

Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Special Issue A: Algorithmic Number Theory Symposium XI , 2014 , pp. 418 - 432
Copyright
© The Author(s) 2014 

References

Ankeny, N. C., ‘The least quadratic non residue’, Ann. of Math. (2) 55 (1952) no. 1, 65–72.CrossRefGoogle Scholar
Bach, E., ‘Explicit bounds for primality testing and related problems’, Math. Comp. 55 (1990) no. 191, 355–380.CrossRefGoogle Scholar
Cassels, J. W. S., ‘Global fields’, Algebraic number theory (eds Cassels, J. W. S. and Frohlich, A.; Academic Press, 1967) 42–84.Google Scholar
Charles, D. X., Lauter, K. E. and Goren, E. Z., ‘Cryptographic hash functions from expander graphs’, J. Cryptology 22 (2009) no. 1, 93–113.CrossRefGoogle Scholar
Cornacchia, G., ‘Su di un metodo per la risoluzione in numeri interi dell’equazione ∑h=0nc hx n−hy h = p’, Giornale di Matematiche di Battaglini 46 (1903) 33–90.Google Scholar
Deuring, M., ‘Die Typen der Multiplikatorenringe elliptischer Funktionenkörper’, Abh. Math. Semin. Univ. Hamb. 14 (1941) 197–272.CrossRefGoogle Scholar
Bosma, W., Cannon, J. J., Fieker, C. and Steel, A. (eds), Handbook of Magma functions, version 2.20 (2013) http://magma.maths.usyd.edu.au/magma/.Google Scholar
Kohel, D., (1996) ‘Endomorphism rings of elliptic curves over finite fields’, PhD Thesis, University of California, Berkeley.Google Scholar
Petit, C., Lauter, K. and Quisquater, J.-J., ‘Full cryptanalysis of LPS and Morgenstern hash functions’, Security and cryptography for networks, Lecture Notes in Computer Science 5229 (eds Ostrovsky, R., De Prisco, R. and Visconti, I.; Springer, Berlin, 2008) 263–277.CrossRefGoogle Scholar
Pizer, A., ‘An algorithm for computing modular forms on Γ 0(N)∗’, J. Algebra 64 (1980) 340–390.CrossRefGoogle Scholar
Vignéras, M.-F., Arithmétique des algèbres de quaternions (Springer, 1980).Google Scholar