Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-05T09:55:12.589Z Has data issue: false hasContentIssue false
  • English
  • Français

On the minimal modules for exceptional Lie algebras: Jordan blocks and stabilizers

Part of: Lie algebras and Lie superalgebras Linear algebraic groups and related topics

Published online by Cambridge University Press:  01 July 2016

David I. Stewart
David I. Stewart*
Affiliation:
School of Mathematics and Statistics, University of Newcastle, Herschel Building, Newcastle NE1 7RU, United Kingdom email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

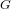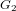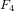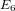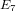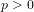Let $G$ be a simple simply connected exceptional algebraic group of type $G_{2}$, $F_{4}$, $E_{6}$ or $E_{7}$ over an algebraically closed field $k$ of characteristic $p>0$ with 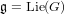$\mathfrak{g}=\text{Lie}(G)$. For each nilpotent orbit 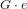$G\cdot e$ of 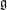$\mathfrak{g}$, we list the Jordan blocks of the action of $e$ on the minimal induced module 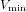$V_{\text{min}}$ of 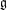$\mathfrak{g}$. We also establish when the centralizers 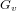$G_{v}$ of vectors 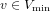$v\in V_{\text{min}}$ and stabilizers 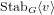$\text{Stab}_{G}\langle v\rangle$ of 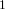$1$-spaces 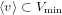$\langle v\rangle \subset V_{\text{min}}$ are smooth; that is, when 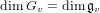$\dim G_{v}=\dim \mathfrak{g}_{v}$ or 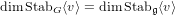$\dim \text{Stab}_{G}\langle v\rangle =\dim \text{Stab}_{\mathfrak{g}}\langle v\rangle$.

MSC classification

Primary: 17B45: Lie algebras of linear algebraic groups 20G15: Linear algebraic groups over arbitrary fields
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Issue 1 , 2016 , pp. 235 - 258
Copyright
© The Author 2016 

References

Azad, H., Barry, M. and Seitz, G., ‘On the structure of parabolic subgroups’, Comm. Algebra 18 (1990) no. 2, 551–562; MR 1047327 (91d:20048).Google Scholar
Bate, M., Martin, B., Röhrle, G. and Tange, R., ‘Complete reducibility and separability’, Trans. Amer. Math. Soc. 362 (2010) no. 8, 4283–4311.CrossRefGoogle Scholar
Bourbaki, N., Éléments de mathématique. Groupes et algèbres de Lie. Chapitres 4, 5 et 6 (Masson, Paris, 1981); MR 0647314.Google Scholar
Cohen, A. M. and Cooperstein, B. N., ‘The 2-spaces of the standard E 6(q)-module’, Geom. Dedicata 25 (1988) no. 1–3, 467–480; Geometries and groups (Noordwijkerhout, 1986), MR 925847 (89c:51013).CrossRefGoogle Scholar
Herpel, S., ‘On the smoothness of centralizers in reductive groups’, Trans. Amer. Math. Soc. 365 (2013) no. 7, 3753–3774; MR 3042602.Google Scholar
Herpel, S. and Stewart, D. I., ‘On the smoothness of normalisers, the subalgebra structure of modular Lie algebras and the cohomology of small representations’, Doc. Math. 21 (2016) 1–37.Google Scholar
Jantzen, J. C., Representations of algebraic groups , 2nd edn, Mathematical Surveys and Monographs 107 (American Mathematical Society, Providence, RI, 2003); MR 2015057 (2004h:20061).Google Scholar
Kleidman, P. B., ‘The maximal subgroups of the Chevalley groups G 2(q) with q odd, the Ree groups 2 G 2(q), and their automorphism groups’, J. Algebra 117 (1988) no. 1, 30–71; MR 955589 (89j:20055).Google Scholar
Lawther, R., ‘Jordan block sizes of unipotent elements in exceptional algebraic groups’, Comm. Algebra 23 (1995) no. 11, 4125–4156; MR 1351124 (96h:20084).Google Scholar
Lawther, R., Correction to: “Jordan block sizes of unipotent elements in exceptional algebraic groups” [Comm. Algebra 23 (1995) no. 11, 4125–4156; MR 1351124 (96h:20084)], Comm. Algebra 26(8) (1998) 2709; MR 1627924 (99f:20073).Google Scholar
Le Halleur, S. P., ‘Subgroups of maximal rank of reductive groups’, Autour des schémas en groupes, Panor. Synthèses (2014) 42–43.Google Scholar
Liebeck, M. W. and Saxl, J., ‘On the orders of maximal subgroups of the finite exceptional groups of Lie type’, Proc. Lond. Math. Soc. (3) 55 (1987) no. 2, 299–330; MR 896223 (89b:20068).Google Scholar
Liebeck, M. W. and Seitz, G. M., Unipotent and nilpotent classes in simple algebraic groups and Lie algebras , Mathematical Surveys and Monographs 180 (American Mathematical Society, Providence, RI, 2012); MR 2883501.Google Scholar
Spaltenstein, N., ‘Nilpotent classes in Lie algebras of type F 4 over fields of characteristic 2’, J. Fac. Sci. Univ. Tokyo Sect. 1A 30 (1984) no. 3, 517–524; MR 731515.Google Scholar
Springer, T. A. and Steinberg, R., ‘Conjugacy classes’, Seminar on algebraic groups and related finite groups (The Institute for Advanced Study, Princeton, N.J., 1968/69) , Lecture Notes in Mathematics 131 (Springer, Berlin, 1970) 167–266; MR 0268192 (42 #3091).Google Scholar
University of Georgia VIGRE Algebra Group: Benson, D. J., Bergonio, P., Boe, B. D., Chastkofsky, L., Cooper, B., Guy, G. M., Hower, J., Hunziker, M., Hyun, J. J., Kujawa, J., Matthews, G., Mazza, N., Nakano, D. K., Platt, K. J. and Wright, C., ‘Varieties of nilpotent elements for simple Lie algebras. II. Bad primes’, J. Algebra 292 (2005) no. 1, 65–99; MR 2166796 (2006k:14083).Google Scholar