Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T04:49:01.055Z Has data issue: false hasContentIssue false
  • English
  • Français

On families of 7- and 11-congruent elliptic curves

Part of: Arithmetic algebraic geometry Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  01 September 2014

Tom Fisher
Tom Fisher*
Affiliation:
University of Cambridge, DPMMS, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WB, United Kingdom email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We use an invariant-theoretic method to compute certain twists of the modular curves 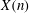$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}X(n)$ for 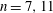$n=7,11$. Searching for rational points on these twists enables us to find non-trivial pairs of $n$-congruent elliptic curves over ${\mathbb{Q}}$, that is, pairs of non-isogenous elliptic curves over ${\mathbb{Q}}$ whose $n$-torsion subgroups are isomorphic as Galois modules. We also find a non-trivial pair of 11-congruent elliptic curves over 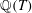${\mathbb{Q}}(T)$, and hence give an explicit infinite family of non-trivial pairs of 11-congruent elliptic curves  over 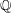${\mathbb{Q}}$.

Supplementary materials are available with this article.

MSC classification

Secondary: 11G05: Elliptic curves over global fields 11F80: Galois representations
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Issue 1 , 2014 , pp. 536 - 564
Copyright
© The Author 2014 

References

Adler, A., ‘Invariants of PSL2(F 11) acting on C 5 ’, Comm. Algebra 20 (1992) no. 10, 2837–2862.Google Scholar
Adler, A. and Ramanan, S., Moduli of abelian varieties , Lecture Notes in Mathematics 1644 (Springer, 1996).CrossRefGoogle Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system I: The user language’, J. Symbolic Comput. 24 (1997) 235–265; see also the Magma home page at http://magma.maths.usyd.edu.au/magma/.Google Scholar
Cremona, J. E., Algorithms for modular elliptic curves (Cambridge University Press, Cambridge, 1997) ; see also http://www.warwick.ac.uk/∼masgaj/ftp/data/.Google Scholar
Cremona, J. E., Fisher, T. A. and Stoll, M., ‘Minimisation and reduction of 2-, 3- and 4-coverings of elliptic curves’, Algebra Number Theory 4 (2010) no. 6, 763–820.CrossRefGoogle Scholar
Cremona, J. E. and Mazur, B., ‘Visualizing elements in the Shafarevich–Tate group’, Experiment. Math. 9 (2000) no. 1, 13–28.Google Scholar
Elkies, N. D., ‘The Klein quartic in number theory’, The eightfold way: The beauty of Klein’s quartic curve , Mathematical Sciences Research Institute Publications 35 (ed. Levy, S.; Cambridge University Press, Cambridge, 1999) 51–101.Google Scholar
Fisher, T. A., ‘On 5 and 7 descents for elliptic curves’, PhD Thesis, University of Cambridge, 2000, http://www.dpmms.cam.ac.uk/∼taf1000/thesis.html.Google Scholar
Fisher, T. A., ‘Some examples of 5 and 7 descent for elliptic curves over Q ’, J. Eur. Math. Soc. 3 (2001) no. 2, 169–201.Google Scholar
Fisher, T. A., ‘The invariants of a genus one curve’, Proc. Lond. Math. Soc. (3) 97 (2008) 753–782.Google Scholar
Fisher, T. A., ‘The Hessian of a genus one curve’, Proc. Lond. Math. Soc. (3) 104 (2012) 613–648.CrossRefGoogle Scholar
Fisher, T. A., ‘Invariant theory for the elliptic normal quintic, I. Twists of X (5)’, Math. Ann. 356 (2013) no. 2, 589–616.Google Scholar
Fisher, T. A., ‘On families of 7- and 11-congruent elliptic curves’, Electronic data accompanying this article, http://journals.cambridge.org/sup_S1461157014000059sup001.Google Scholar
Frey, G., ‘On elliptic curves with isomorphic torsion structures and corresponding curves of genus 2’, Elliptic curves, modular forms & Fermat’s Last Theorem, Hong Kong, 1993 , Series on Number Theory I (eds Coates, J. and Yau, S.-T.; International Press, Cambridge, MA, 1995) 79–98.Google Scholar
Halberstadt, E. and Kraus, A., ‘On the modular curves Y E (7)’, Math. Comp. 69 (2000) no. 231, 1193–1206.Google Scholar
Halberstadt, E. and Kraus, A., ‘Sur la courbe modulaire X E (7)’, Experiment. Math. 12 (2003) no. 1, 27–40.Google Scholar
Kani, E. J. and Rizzo, O. G., ‘Mazur’s question on mod 11 representations of elliptic curves’, Preprint, http://www.mast.queensu.ca/∼kani/mdqs.htm.Google Scholar
Kani, E. and Schanz, W., ‘Modular diagonal quotient surfaces’, Math. Z. 227 (1998) no. 2, 337–366.Google Scholar
Klein, F., ‘Über die Transformationen siebenter Ordnung der elliptischen Funktionen’, Math. Ann. 14 (1878) 428–471; English translation in The eightfold way: The beauty of Klein’s quartic curve, Mathematical Sciences Research Institute Publications 35 (ed. S. Levy; Cambridge University Press, Cambridge 1999).Google Scholar
Klein, F., ‘Über die Transformationen elfter Ordnung der elliptischen Funktionen’, Math. Ann. 15 (1879) Reprinted in Gesammelte Mathematische Abhandlungen III (ed. R. Fricke et al.; Springer, 1923) 140–168.Google Scholar
Klein, F., ‘Über die elliptischen Normalkurven der n-ten Ordnung’ (1885); Reprinted in Gesammelte Mathematische Abhandlungen III (ed. R. Fricke et al.; Springer, 1923) 198–254.Google Scholar
Kraus, A. and Oesterlé, J., ‘Sur une question de B. Mazur’, Math. Ann. 293 (1992) no. 2, 259–275.Google Scholar
Mazur, B., ‘Rational isogenies of prime degree’, Invent. Math. 44 (1978) no. 2, 129–162.Google Scholar
Mumford, D., ‘Varieties defined by quadratic equations’, Questions on algebraic varieties (C.I.M.E., III Ciclo, Varenna, 1969) (Edizioni Cremonese, Rome, 1970) 29–100.Google Scholar
Papadopoulos, I., ‘Courbes elliptiques ayant même 6-torsion qu’une courbe elliptique donnée’, J. Number Theory 79 (1999) no. 1, 103–114.Google Scholar
Poonen, B., Schaefer, E. F. and Stoll, M., ‘Twists of X (7) and primitive solutions to x 2 + y 3 = z 7 ’, Duke Math. J. 137 (2007) no. 1, 103–158.Google Scholar
Ribet, K. A., ‘Raising the levels of modular representations’, Séminaire de Théorie des Nombres, Paris, 1987–1988 , Progress in Mathematics 81 (ed. Goldstein, C.; Birkhäuser, Boston, 1990) 259–271.Google Scholar
Rubin, K. and Silverberg, A., ‘Families of elliptic curves with constant mod p representations’, Elliptic curves, modular forms & Fermat’s Last Theorem, Hong Kong, 1993 , Series in Number Theory I (eds Coates, J. and Yau, S.-T.; International Press, Cambridge, MA, 1995) 148–161.Google Scholar
Rubin, K. and Silverberg, A., ‘Mod 6 representations of elliptic curves’, Automorphic Forms, Automorphic representations, and arithmetic, Fort Worth, TX, 1996 , Proceedings of Symposia in Pure Mathematics, Part 1 66 (American Mathematical Society, Providence, RI, 1999) 213–220.CrossRefGoogle Scholar
Rubin, K. and Silverberg, A., ‘Mod 2 representations of elliptic curves’, Proc. Amer. Math. Soc. 129 (2001) no. 1, 53–57.Google Scholar
Silverberg, A., ‘Explicit families of elliptic curves with prescribed mod N representations’, Modular forms and Fermat’s last theorem, Boston, MA, 1995 (eds Cornell, G., Silverman, J. H. and Stevens, G.; Springer-Verlag, New York, 1997) 447–461.CrossRefGoogle Scholar
Silverman, J. H., The arithmetic of elliptic curves , Graduate Text in Mathematics 106 (Springer, New York, 1986).Google Scholar
Vélu, J., ‘Isogénies entre courbes elliptiques’, C. R. Math. Acad. Sci. Paris 273 (1971) 238–241.Google Scholar
Vélu, J., ‘Courbes elliptique munies d’un sous-group ℤ∕nℤ × μ n ’, Mém. Soc. Math. Fr. 57 (1978).Google Scholar
Supplementary material: File

Fisher Supplementary Material

Supplementary Material

Download Fisher Supplementary Material(File)
File 51.3 KB