Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T07:40:35.807Z Has data issue: false hasContentIssue false
  • English
  • Français

On a conjecture of Rudin on squares in arithmetic progressions

Part of: Curves Arithmetic algebraic geometry Sequences and sets Diophantine equations

Published online by Cambridge University Press:  01 April 2014

Enrique González-Jiménez  and
Xavier Xarles
Enrique González-Jiménez
Affiliation:
Universidad Autónoma de Madrid Departamento de Matemáticas and Instituto de Ciencias Matemáticas (ICMat), Madrid, Spain email [email protected]
Xavier Xarles
Affiliation:
Departament de Matemàtiques Universitat Autònoma de Barcelona, 08193 Bellaterra Barcelona, Catalonia email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 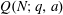$Q(N;q,a)$ be the number of squares in the arithmetic progression 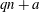$qn+a$, for 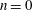$n=0$,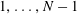$1,\ldots,N-1$, and let 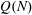$Q(N)$ be the maximum of 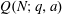$Q(N;q,a)$ over all non-trivial arithmetic progressions 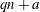$qn + a$. Rudin’s conjecture claims that 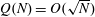$Q(N)=O(\sqrt{N})$, and in its stronger form that 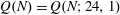$Q(N)=Q(N;24,1)$ if 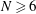$N\ge 6$. We prove the conjecture above for 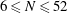$6\le N\le 52$. We even prove that the arithmetic progression 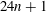$24n+1$ is the only one, up to equivalence, that contains 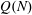$Q(N)$ squares for the values of 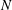$N$ such that 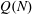$Q(N)$ increases, for 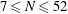$7\le N\le 52$ (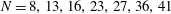$N=8,13,16,23,27,36,41$ and 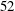$52$).

Supplementary materials are available with this article.

MSC classification

Secondary: 11G30: Curves of arbitrary genus or genus $ne 1$ over global fields 11B25: Arithmetic progressions 11D45: Counting solutions of Diophantine equations 14H25: Arithmetic ground fields
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Issue 1 , 2014 , pp. 58 - 76
Copyright
© The Author(s) 2014 

References

Modular Functions of One Variable IV , Lecture Notes in Mathematics 476 (eds Birch, B. J. and Kuyk, W.; (Springer, 1975).Google Scholar
Bombieri, E., Granville, A. and Pintz, J., ‘Squares in arithmetic progressions’, Duke Math. J. 66 (1992) 369–385.Google Scholar
Bombieri, E. and Zannier, U., ‘A note on squares in arithmetic progressions. II’, Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Rend. Lincei (9) Mat. Appl. 13 (2002) 69–75.Google Scholar
W. Bosma, J. Cannon, C. Fieker, and A. Steel (eds), ‘Handbook of Magma functions, Edition 2.18-8’, 2012, http://magma.maths.usyd.edu.au/magma.Google Scholar
Bruin, N., ‘Chabauty methods using elliptic curves’, J. Reine Angew. Math. 562 (2003) 27–49.Google Scholar
Bruin, N. and Stoll, M., ‘Two-cover descent on hyperelliptic curves’, Math. Comp. 78 (2009) 2347–2370.Google Scholar
Caporaso, L., Harris, J. and Mazur, B., ‘Uniformity of rational points’, J. Amer. Math. Soc. 10 (1997) 1–35.Google Scholar
Chabauty, C., ‘Sur les points rationnels des courbes algébriques de genre supérieur à l’unité’, C. R. Acad. Sci. Paris 212 (1941) 882–885.Google Scholar
Chevalley, C. and Weil, A., ‘Un théorème d’arithmétique sur les courbes algébriques’, C. R. Acad. Sci. Paris 195 (1932) 570–572.Google Scholar
Cohn, J. H. E., ‘Squares in arithmetical progressions. I, II’, Math. Scand. 52 (1983) 5–19; 20–23.CrossRefGoogle Scholar
Coleman, R F, ‘Effective Chabauty’, Duke Math. J. 52 (1985) 765–770.Google Scholar
Coombes, K. R. and Grant, D. R., ‘On heterogeneous spaces’, J. London Math. Soc. (2) 40 (1989) 385–397.Google Scholar
Cremona, J. E., Algorithms for modular elliptic curves (Cambridge University Press, 1992).Google Scholar
Erdős, P., ‘Quelques problèmes de théorie des nombres’, Monographies de L’Enseignement Mathématique, No. 6, (L’Enseignement Mathématique, Université, Geneva, 1963) 81–135.Google Scholar
Flynn, E. V., ‘A flexible method for applying Chabauty’s Theorem’, Compositio Math. 105 (1997) 79–94.Google Scholar
Flynn, E. V. and Wetherell, J. L., ‘Covering collections and a challenge problem of Serre’, Acta Arith. 98 (2001) 197–205.CrossRefGoogle Scholar
González-Jiménez, E. and Xarles, X., ‘On symmetric square values of quadratic polynomials’, Acta Arith. 149 (2011) 145–159.Google Scholar
González-Jiménez, E. and Xarles, X., ‘Five squares in arithmetic progression over quadratic fields’, Rev. Mat. Iberoam. 29 (2013) 1211–1238.Google Scholar
Halberstadt, E., ‘Signes locaux des courbes elliptiques en 2 et 3’, C. R. Acad. Sci. Paris Sér. I Math. 326 (1998) 1047–1052.Google Scholar
Kulesz, L., ‘Courbes algébriques de genre $\geq $ 2 possédant de nombreux points rationnels’, Acta Arith. 87 (1998) 103–120.Google Scholar
McCallum, W. and Poonen, B., ‘On the method of Chabauty and Coleman’, Explicit methods in number theory: rational points and Diophantine equations , Panoramas et Syntèses 36 (Société Mathématique de France, 2012).Google Scholar
Rohrlich, D. E., ‘Variation of the root number in families of elliptic curves’, Compositio Math. 87 (1993) 119–151.Google Scholar
Rudin, W., ‘Trigonometric series with gaps’, J. Math. Mech. 9 (1960) 203–227.Google Scholar
Sloane, N., ‘The On-Line Encyclopedia of Integer Sequences’, http://oeis.org/.Google Scholar
Stoll, M., ‘Independence of rational points on twists of a given curve’, Compos. Math. 142 (2006) 1201–1214.Google Scholar
Stoll, M., ‘Finite descent obstructions and rational points on curves’, Algebra Number Theory 1 (2007) 349–391.Google Scholar
Szemerédi, E., ‘The number of squares in an arithmetic progression’, Studia Sci. Math. Hungar. 9 (1975) 417.Google Scholar
Wetherell, J. L., ‘Bounding the number of rational points on certain curves of high rank’, PhD Thesis, University of California, Berkeley, 1997.Google Scholar
Xarles, X., ‘Squares in arithmetic progression over number fields’, J. Number Theory 132 (2012) 379–389.Google Scholar
Supplementary material: File

González-Jiménez and Xarles Supplementary Material

Supplementary Material

Download González-Jiménez and Xarles Supplementary Material(File)
File 37.5 MB