A note on magnitude bounds for the mask coefficients of the interpolatory Dubuc–Deslauriers subdivision scheme

Abstract

We analyse the mask associated with the 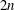$2n$-point interpolatory Dubuc–Deslauriers subdivision scheme 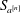$S_{a^{[n]}}$. Sharp bounds are presented for the magnitude of the coefficients 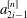$a^{[n]}_{2i-1}$ of the mask. For scales 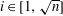$i \in [1,\sqrt{n}]$ it is shown that 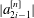$|a^{[n]}_{2i-1}|$ is comparable to 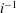$i^{-1}$, and for larger power scales, exponentially decaying bounds are obtained. Using our bounds, we may precisely analyse the summability of the mask as a function of $n$ by identifying which coefficients of the mask contribute to the essential behaviour in $n$, recovering and refining the recent result of Deng–Hormann–Zhang that the operator norm of 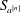$S_{a^{[n]}}$ on 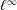$\ell ^\infty $ grows logarithmically in $n$.