Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T07:53:50.709Z Has data issue: false hasContentIssue false
  • English
  • Français

The multiple number field sieve for medium- and high-characteristic finite fields

Part of: Finite fields and commutative rings (number-theoretic aspects) Computational number theory

Published online by Cambridge University Press:  01 August 2014

Razvan Barbulescu  and
Cécile Pierrot
Razvan Barbulescu
Affiliation:
Université de Lorraine, France email [email protected]
Cécile Pierrot
Affiliation:
Laboratoire d’Informatique de Paris 6, UPMC, France email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study the discrete logarithm problem in medium- and high-characteristic finite fields. We propose a variant of the number field sieve (NFS) based on numerous number fields. Our improved algorithm computes discrete logarithms in 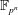$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{F}_{p^n}$ for the whole range of applicability of the NFS and lowers the asymptotic complexity from 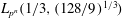$L_{p^n}({1/3},({128/9})^{1/3})$ to 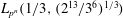$L_{p^n}({1/3},(2^{13}/3^6)^{1/3})$ in the medium-characteristic case, and from 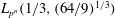$L_{p^n}({1/3},({64/9})^{1/3})$ to 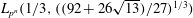$L_{p^n}({1/3},((92 + 26 \sqrt{13})/27)^{1/3})$ in the high-characteristic case.

MSC classification

Secondary: 11T99: None of the above, but in this section 11Y16: Algorithms; complexity
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Special Issue A: Algorithmic Number Theory Symposium XI , 2014 , pp. 230 - 246
Copyright
© The Author(s) 2014 

References

Barbulescu, R., ‘Algorithmes de logarithmes discrets dans les corps finis’. PhD Thesis, Université de Lorraine, 2013.Google Scholar
Bernstein, D. J., ‘The multiple-lattice number field sieve’, Technical report, University of California, Berkeley, 1991.Google Scholar
Boneh, D. and Franklin, M. K., ‘Identity-based encryption from the Weil pairing’, SIAM J. Comput. 32 (2003) no. 3, 586–615.Google Scholar
Barbulescu, R., Gaudry, P., Joux, A. and Thomé, E., ‘A heuristic quasi-polynomial algorithm for discrete logarithm in finite fields of small characteristic’, Advances in cryptology – EUROCRYPT 2014, Lecture Notes in Computer Science 8441 (Springer, 2014) 1–16.Google Scholar
Canfield, E. R., Erdős, P. and Pomerance, C., ‘On a problem of Oppenheim concerning factorisatio numerorum’, J. Number Theory 17 (1983) 1–28.CrossRefGoogle Scholar
Coppersmith, D., ‘Modifications to the number field sieve’, J. Cryptology 6 (1993) no. 3, 169–180.CrossRefGoogle Scholar
Commeine, A. and Semaev, I., ‘An algorithm to solve the discrete logarithm problem with the number field sieve’, Public key cryptology – PKC 2006, Lecture Notes in Computer Science 3958 (Springer, 2006) 174–190.CrossRefGoogle Scholar
Diffie, W. and Hellman, M. E., ‘New directions in cryptography’, IEEE Trans. Inf. Theory 22 (1976) no. 6, 644–654.CrossRefGoogle Scholar
ElGamal, T., ‘A public key cryptosystem and a signature scheme based on discrete logarithms’, IEEE Trans. Inform. Theory 31 (1985) no. 4, 469–472.CrossRefGoogle Scholar
Elkenbracht-Huizing, R. M., ‘A multiple polynomial general number field sieve’, Algorithmic number theory, Lecture Notes in Computer Science 1122 (ed. Cohen, H.; Springer, 1996) 99–114.CrossRefGoogle Scholar
Fiat, A. and Shamir, A., ‘How to prove yourself: practical solutions to identification and signature problems’, Advances in cryptology – CRYPTO ’86, Lecture Notes in Computer Science 263 (Springer, 1986) 186–194.Google Scholar
Joux, A., ‘A one round protocol for tripartite Diffie–Hellman’, J. Cryptology 17 (2004) no. 4, 263–276.CrossRefGoogle Scholar
Joux, A. and Lercier, R., ‘Improvements to the general number field sieve for discrete logarithms in prime fields. A comparison with the Gaussian integer method’, Math. Comput. 72 (2003) no. 242, 953–967.Google Scholar
Joux, A., Lercier, R., Smart, N. P. and Vercauteren, F., ‘The number field sieve in the medium prime case’, Advances in cryptology – CRYPTO 2006, Lecture Notes in Computer Science 4117 (Springer, 2006) 326–344.Google Scholar
Joux, A. and Pierrot, C., ‘The special number field sieve in Fp n, application to pairing-friendly constructions’, Pairing-based cryptography – Pairing 2013, Lecture Notes in Computer Science 8365 (Springer, 2013) 45–61.Google Scholar
Matyukhin, D. V., ‘On asymptotic complexity of computing discrete logarithms over G F (p)’, Discrete Math. Appl. 13 (2003) no. 1, 27–50.CrossRefGoogle Scholar
Paillier, P., ‘Public-key cryptosystems based on composite degree residuosity classes’, Advances in cryptology – Eurocrypt ’99, Lecture Notes in Computer Science 1592 (Springer, 1999) 223–238.Google Scholar
Stein, W. A. et al. , Sage Mathematics Software (Version 5.8). The Sage Development Team, 2013, http://www.sagemath.org.Google Scholar
Schnorr, C.-P., ‘Efficient identification and signatures for smart cards’, Advances in cryptology – CRYPTO ’89, Lecture Notes in Computer Science 435 (Springer, 1990) 239–252.Google Scholar
Schirokauer, O., ‘Using number fields to compute logarithms in finite fields’, Math. Comput. 69 (2000) no. 231, 1267–1283.CrossRefGoogle Scholar
von zur Gathen, J. and Gerhard, J., Modern computer algebra, 3rd edn (Cambridge University Press, 2013).CrossRefGoogle Scholar
Wiedemann, D., ‘Solving sparse linear equations over finite fields’, IEEE Trans. Inform. Theory 32 (1986) no. 1, 54–62.CrossRefGoogle Scholar