Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T05:51:18.041Z Has data issue: false hasContentIssue false
  • English
  • Français

Modular subgroups, dessins d’enfants and elliptic K3 surfaces

Part of: Surfaces and higher-dimensional varieties Discontinuous groups and automorphic forms Arithmetic algebraic geometry

Published online by Cambridge University Press:  01 August 2013

Yang-Hui He ,
John McKay  and
James Read
Yang-Hui He
Affiliation:
Department of Mathematics,City University,Northampton Square,London EC1V 0HB,United Kingdom email [email protected] School of Physics,NanKai University,Tianjin, 300071,PR China email [email protected] Merton College,University of Oxford,Oxford OX1 4JD,United Kingdom email [email protected]
John McKay
Affiliation:
Department of Mathematics and Statistics,Concordia University,1455 de Maisonneuve Boulevard,West Montreal, Quebec, H3G 1M8,Canada email [email protected]
James Read
Affiliation:
Oriel College,University of Oxford,Oxford OX1 4EW,United Kingdom email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the 33 conjugacy classes of genus zero, torsion-free modular subgroups, computing ramification data and Grothendieck’s dessins d’enfants. In the particular case of the index 36 subgroups, the corresponding Calabi–Yau threefolds are identified, in analogy with the index 24 cases being associated to K3 surfaces. 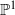In a parallel vein, we study the 112 semi-stable elliptic fibrations over ${ \mathbb{P} }^{1} $ as extremal K3 surfaces with six singular fibres. In each case, a representative of the corresponding class of subgroups is identified by specifying a generating set for that representative.

MSC classification

Secondary: 11G32: Dessins d'enfants, Belyĭ theory 11F06: Structure of modular groups and generalizations; arithmetic groups 14J32: Calabi-Yau manifolds 14J28: $K3$ surfaces and Enriques surfaces
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 16 , October 2013 , pp. 271 - 318
Copyright
© The Author(s) 2013 

References

Ashok, S., Cachazo, F. and Dell’Aquila, E., ‘Children’s drawings from Seiberg–Witten curves’, Preprint, 2006, arXiv:hep-th/0611082v1.Google Scholar
Beukers, F. and Montanus, H., ‘Explicit calculation of elliptic fibrations of K3-surfaces and their Belyi-maps’, Number theory and polynomials, LMS Lecture Note Series 352 (Cambridge University Press, Cambridge, 2008) 33–51.Google Scholar
Beukers, F., ‘Dessins coming from the Miranda–Persson table’, 2008, available at http://www.staff.science.uu.nl/~beuke106/mirandapersson/Dessins.html.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The MAGMA algebra system. I. The user language’, J. Symbolic Comput. 24 (1997) 235–265.Google Scholar
Conder, M., ‘Schreier coset graphs and their applications’, RIMS Kokyuroku 794 (1992) 169–175.Google Scholar
Conway, J., Hulpke, A. and McKay, J., ‘On transitive permutation groups’, LMS J. Comput. Math. 1 (1996) 1–8.Google Scholar
The GAP group, ‘GAP—Groups, algorithms, and programming, version 4.5.6’, 2012, http://www.gap-system.org.Google Scholar
He, Y.-H. and McKay, J., ‘ $ \mathcal{N} = 2$ gauge theories: congruence subgroups, coset graphs and modular surfaces’, J. Math. Phys. 54 (2013) 012301.Google Scholar
Holt, D., Eick, B. and O’Brien, E., Handbook of computational group theory, Discrete Mathematics and Its Applications (Chapman and Hall, London, 2005).Google Scholar
Lando, S. and Zvonkin, A., ‘Graphs on surfaces and their applications’, Low-dimensional topology II, Encyclopaedia of Mathematical Sciences 141 (Springer, New York, 2004).Google Scholar
McKay, J. and Sebbar, A., ‘J-invariants of arithmetic semistable elliptic surfaces and graphs’, Proceedings on Moonshine and related topics, Montréal, QC, 1999, CRM Proceedings and Lecture Notes 30 (American Mathematical Society, New York, 2001) 119–130.Google Scholar
Miranda, R. and Persson, U., ‘Configurations of in fibers on elliptic K3-surfaces’, Math. Z. 201 (1989) 339–361.Google Scholar
Morrison, D. and Vafa, C., ‘Compactifications of F theory on Calabi–Yau threefolds - I’, Nucl. Phys. B 473 (1996).Google Scholar
Morrison, D. and Vafa, C., ‘Compactifications of F theory on Calabi–Yau threefolds - II’, Nucl. Phys. B 476 (1996).Google Scholar
The Sage Group, ‘Sage—version 5.3’, 2012, http://www.sagemath.org/.Google Scholar
Schneps (ed.), L., The Grothendieck theory of dessins d’enfants, LMS Lecture Note Series 200 (Cambridge University Press, Cambridge, 1994).Google Scholar
Sebbar, A., ‘Modular subgroups, forms, curves and surfaces’, Canad. Math. Bull. 45 (2002) 294–308.Google Scholar
Shioda, T., ‘On elliptic modular surfaces’, J. Math. Soc. Japan 24 (1972) 20–59.Google Scholar
Singerman, D. and Wolfart, J., ‘Cayley graphs, Cori hypermaps, and dessins d’enfants’, Ars Math. Contemp. 1 (2008) 144–153.Google Scholar
Top, J. and Yui, N., ‘Explicit equations of some elliptic modular surfaces’, Rocky Mountain J. Math. 37 (2007) 663–687.Google Scholar
Zvonkin, A., ‘Functional composition is a generalized symmetry’, Symmetry: Culture Sci. 22 (2011) 391–426.Google Scholar