Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T21:02:22.401Z Has data issue: false hasContentIssue false
  • English
  • Français

Modular elliptic curves over the field of twelfth roots of unity

Part of: Arithmetic algebraic geometry Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  01 April 2016

Andrew Jones
Andrew Jones*
Affiliation:
School of Mathematics and Statistics, University of Sheffield, Hounsfield Road, SheffieldS3 7RH, United Kingdom email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we perform an extensive study of the spaces of automorphic forms for 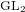$\text{GL}_{2}$ of weight $2$ and level $\mathfrak{n}$, for $\mathfrak{n}$ an ideal in the ring of integers of the quartic CM field 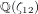$\mathbb{Q}({\it\zeta}_{12})$ of twelfth roots of unity. This study is conducted through the computation of the Hecke module 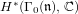$H^{\ast }({\rm\Gamma}_{0}(\mathfrak{n}),\mathbb{C})$, and the corresponding Hecke action. Combining this Hecke data with the Faltings–Serre method for proving equivalence of Galois representations, we are able to provide the first known examples of modular elliptic curves over this field.

Supplementary materials are available with this article.

MSC classification

Primary: 11F41: Automorphic forms on $(2)$; Hilbert and Hilbert-Siegel modular groups and their modular and automorphic forms; Hilbert modular surfaces 11G05: Elliptic curves over global fields 11F80: Galois representations
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Issue 1 , 2016 , pp. 155 - 174
Copyright
© The Author 2016 

References

Ash, A., Gunnells, P. E. and McConnell, M., ‘Resolutions of the Steinberg module for GL(n)’, J. Algebra 349 (2012) 380–390.Google Scholar
Ash, A., Gunnells, P. E. and McConnell, M., ‘Mod 2 homology of GL(4) and Galois representations’, J. Number Theory 146 (2015) 4–22.Google Scholar
Berger, T. and Harcos, G., ‘ ℓ-adic representations associated to modular forms over imaginary quadratic fields’, Int. Math. Res. Not. IMRN 23 (2007) Art. ID rnm113.Google Scholar
Blasius, D. and Rogawski, J., ‘Galois representations for Hilbert modular forms’, Bull. Amer. Math. Soc. (N.S.) 21 (1989) no. 1, 65–69.Google Scholar
Borel, A. and Serre, J. P., ‘Corners and arithmetic groups’, Comment. Math. Helv. 48 (1973) 436–491; with an appendix, ‘Arrondissement des variétés à coins’, by A. Douady and L. Hérault.Google Scholar
Bump, D., Automorphic forms and representations , Cambridge Studies in Advanced Mathematics 55 (Cambridge University Press, Cambridge, 1998).Google Scholar
Carayol, H., ‘Sur les représentations ℓ-adiques associées aux formes modulaires de Hilbert’, Ann. Sci. Éc. Norm. Supér. (4) 19 (1986) 409–468.Google Scholar
Carayol, H., ‘Modular forms and Galois representations with values in a complete local ring’, Contemp. Math. 165 (1994) 213–237.Google Scholar
Chênevert, G., ‘Exponential sums, hypersurfaces with many symmetries and Galois representations’, PhD Thesis, McGill University, Montreal, 2008.Google Scholar
Computational Algebra Group, University of Sydney, ‘MAGMA, Version 2.20-9’, 2014, http://magma.maths.usyd.edu.au/magma.Google Scholar
Donnelly, S., Gunnells, P. E., Klages-Mundt, A. and Yasaki, D., ‘A table of elliptic curves over the cubic field of discriminant − 23’, Exp. Math. 24 (2015) no. 4, 375–390.Google Scholar
Dieulefait, L. V., Guerberoff, L. and Pacetti, A., ‘Proving modularity for a given elliptic curve over an imaginary quadratic field’, Math. Comp. 79 (2010) 1145–1170.Google Scholar
Freitas, N., Le Hung, B. and Siksek, S., ‘Elliptic curves over real quadratic fields are modular’, Invent. Math. 201 (2015) 159–206.Google Scholar
Gunnells, P. E., Hajir, F. and Yasaki, D., ‘Modular forms and elliptic curves over the field of fifth roots of unity’, Exp Math. 22 (2013) no. 2, 203–216.Google Scholar
Gunnells, P. E., ‘Computing Hecke eigenvalues below the cohomological dimension’, Exp. Math. 9 (2000) no. 3, 351–367.Google Scholar
Gunnells, P. E., ‘Lectures on computing cohomology of arithmetic groups’, Computations with modular forms , Contributions in Mathematical and Computational Sciences 6 (Springer, Cham, 2014) 3–45.Google Scholar
Gunnells, P. E. and Yasaki, D., ‘Modular forms and elliptic curves over the cubic field of discriminant 23’, Int. J. Number Theory 9 (2013) no. 1, 53–76.Google Scholar
Harder, G., ‘Eisenstein cohomology of arithmetic groups. The case GL2 ’, Invent. Math. 89 (1987) 37–118.Google Scholar
Harder, G., ‘Cohomology of arithmetic groups’, 2006,http://www.math.uni-bonn.de/people/harder/Manuscripts/.Google Scholar
Hida, H., Elementary theory of L-functions and Eisenstein series , London Mathematical Society Student Texts 26 (Cambridge University Press, Cambridge, 1993).Google Scholar
Harris, M., Lan, K. W., Taylor, R. and Thorne, J., ‘On the rigid cohomology of certain Shimura varieties’, Preprint, 2013, http://www.math.ias.edu/∼rtaylor/rigcoh.pdf.Google Scholar
Harris, M., Soudry, D. and Taylor, R., ‘ ℓ-adic representations associated to modular forms over imaginary quadratic fields. I. Lifting to GSp4(ℚ)’, Invent. Math. 112 (1993) no. 2, 377–411.Google Scholar
Jarvis, F. and Manoharmayum, J., ‘On the modularity of supersingular elliptic curves over certain totally real number fields’, J. Number Theory 128 (2008) no. 3, 589–618.CrossRefGoogle Scholar
Jones, A., ‘Modular elliptic curves over quartic CM fields’, PhD Thesis, University of Sheffield, 2015,http://tberger.staff.shef.ac.uk/Jones_thesis.pdf.Google Scholar
Koecher, M., ‘Beiträge zu einer Reduktionstheorie in Positivitätsbereichen. I’, Math. Ann. 141 (1960) 384–432.Google Scholar
Mok, C. P., ‘Galois representations attached to automorphic forms on GL2 over CM fields’, Compos. Math. 150 (2014) no. 4, 523–567.Google Scholar
Scholze, P., ‘On torsion in the cohomology of locally symmetric varieties’, Ann. of Math. (2) 182 (2015) no. 3, 945–1066.Google Scholar
Schwermer, J., ‘The cohomological approach to cuspidal automorphic representations’, Cont. Math. 488 (2006) 257–285.Google Scholar
Stein, W., Modular forms, a computational approach , Graduate Studies in Mathematics 79 (American Mathematical Society, Providence, RI, 2007), with an appendix by Paul E. Gunnells.Google Scholar
Taylor, R., ‘On Galois representations associated to Hilbert modular forms’, Invent. Math. 98 (1989) 265–280.Google Scholar
Taylor, R., ‘ ℓ-adic representations associated to modular forms over imaginary quadratic fields. II’, Invent. Math. 116 (1994) 619–643.Google Scholar
Supplementary material: File

Jones supplemtary material

PDF of Tabular Data

Download Jones supplemtary material(File)
File 261.1 KB