No CrossRef data available.
Article contents
Heuristics on pairing-friendly abelian varieties
Part of:
Multiplicative number theory
Arithmetic algebraic geometry
Abelian varieties and schemes
Finite fields and commutative rings (number-theoretic aspects)
Published online by Cambridge University Press: 01 June 2015
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We discuss heuristic asymptotic formulae for the number of isogeny classes of pairing-friendly abelian varieties of fixed dimension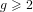 
$g\geqslant 2$ over prime finite fields. In each formula, the embedding degree 
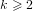$k\geqslant 2$ is fixed and the rho-value is bounded above by a fixed real 
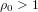${\it\rho}_{0}>1$. The first formula involves families of ordinary abelian varieties whose endomorphism ring contains an order in a fixed CM-field 
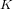$K$ of degree 
$g$ and generalizes previous work of the first author when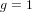 
$g=1$. It suggests that, when 
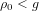${\it\rho}_{0}<g$, there are only finitely many such isogeny classes. On the other hand, there should be infinitely many such isogeny classes when 
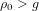${\it\rho}_{0}>g$. The second formula involves families whose endomorphism ring contains an order in a fixed totally real field 
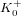$K_{0}^{+}$ of degree 
$g$. It suggests that, when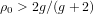 
${\it\rho}_{0}>2g/(g+2)$ (and in particular when 
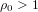${\it\rho}_{0}>1$ if 
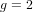$g=2$), there are infinitely many isogeny classes of 
$g$-dimensional abelian varieties over prime fields whose endomorphism ring contains an order of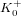 
$K_{0}^{+}$. We also discuss the impact that polynomial families of pairing-friendly abelian varieties has on our heuristics, and review the known cases where they are expected to provide more isogeny classes than predicted by our heuristic formulae.
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2015
References
Balasubramanian, R. and Koblitz, N., ‘The improbability that an elliptic curve has subexponential discrete log problem under the Menezes–Okamoto–Vanstone algorithm’, J. Cryptology
11 (1998) 141–145.Google Scholar
Barreto, P. and Naehrig, M., ‘Pairing-friendly elliptic curves of prime order’,
Selected areas in cryptography (SAC 2005)
, Lecture Notes in Computer Science 3897 (Springer, Berlin, 2006) 319–331.Google Scholar
Bateman, P. T. and Horn, R. A., ‘A heuristic asymptotic formula concerning the distribution of prime numbers’, Math. Comp.
16 (1962) 363–367.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput.
24 (1997) 235–265.Google Scholar
Boxall, J., ‘Heuristics on pairing-friendly elliptic curves’, J. Math. Cryptol.
6 (2012) 81–104.Google Scholar
Brezing, F. and Weng, A., ‘Elliptic curves suitable for pairing based cryptography’, Des. Codes Cryptogr.
37 (2005) 133–141.Google Scholar
Cohen, S. D., ‘The distribution of Galois groups and Hilbert’s irreducibility theorem’, Proc. Lond. Math. Soc.
43 (1981) 227–250.Google Scholar
Conrad, K., ‘Hardy–Littlewood constants’,
Mathematical properties of sequences and other combinatorical structures (Los Angeles, CA, 2002)
(Kluwer Academic, Boston, MA, 2003) 133–154.CrossRefGoogle Scholar
Enge, A. and Sutherland, A. V., ‘Class invariants by the CRT method’,
Algorithmic number theory (ANTS 9)
, Lecture Notes in Computer Science 6197 (Springer, Berlin, 2010) 142–156.Google Scholar
Freeman, D., ‘A generalized Brezing–Weng method for constructing pairing-friendly ordinary abelian varieties’,
Pairing-based cryptography: Pairing 2008
, Lecture Notes in Computer Science 5209 (Springer, Berlin, 2008) 146–163.Google Scholar
Freeman, D., Scott, M. and Teske, E., ‘A taxonomy of pairing-friendly elliptic curves’, J. Cryptology
23 (2010) 224–280.Google Scholar
Freeman, D., Stevenhagen, P. and Streng, M., ‘Abelian varieties with prescribed embedding degree’,
Algorithmic number theory (ANTS 8)
, Lecture Notes in Computer Science 5011 (Springer, Berlin, 2008) 60–73.Google Scholar
Galbraith, S., McKee, J. and Valença, P. C., ‘Ordinary abelian varieties having small embedding degree’, Finite Fields Appl.
13 (2007) 800–814.Google Scholar
Honda, T., ‘Isogeny classes of abelian varieties over finite fields’, J. Math. Soc. Japan
20 (1968) 83–95.Google Scholar
Jiménez Urroz, J., Luca, F. and Shparlinski, I., ‘On the number of isogeny classes and pairing-friendly elliptic curves and statistics for MNT curves’, Math. Comp.
81 (2012) 1093–1110.Google Scholar
Kohel, D., ‘Echidna databases. Databases for elliptic curves and higher dimensional analogues’,http://echidna.maths.usyd.edu.au/∼kohel/dbs/.Google Scholar
Landau, E.,
Handbuch der Lehre von der Verteilung der Primzahlen
(Teubner, Leipzig, 1909).Google Scholar
Lauter, K. and Shang, N., ‘Generating pairing-friendly parameters for the CM construction of genus 2 curves over prime fields’, Des. Codes Cryptogr.
67 (2013) no. 3, 341–355.Google Scholar
Luca, F. and Shparlinski, I., ‘Elliptic curves of low embedding degree’, J. Cryptology
19 (2006) 553–562.Google Scholar
Narkiewicz, W.,
Elementary and analytic theory of algebraic numbers
(Polish Scientific, Warsaw, 1974).Google Scholar
Rubin, K. and Silverberg, A., ‘Using abelian varieties to improve pairing-based cryptography’, J. Cryptology
22 (2009) 330–364.Google Scholar
Shimura, G., ‘Abelian varieties with complex multiplication and modular functions’, Princeton Mathematical Series 46 (Princeton University Press, Princeton, NJ, 1997).Google Scholar
Tate, J. T., ‘Endomorphisms of abelian varieties over finite fields’, Invent. Math.
2 (1966) 134–144.Google Scholar
Tate, J. T.,
Classes d’isogénie des variétés abéliennes sur un corps fini (d’aprés T. Honda), Séminaire Bourbaki, vol. 1968/69: Exposés 347–363
, Lecture Notes in Mathematics 179 (Springer, Berlin, 1971) 95–110. Exp. 352.Google Scholar
Waterhouse, W. C., ‘Abelian varieties over finite fields’, Ann. Sci. Éc. Norm. Supér. (4)
2 (1969) 521–560.Google Scholar
You have
Access