Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T12:05:18.992Z Has data issue: false hasContentIssue false
  • English
  • Français

Finding roots in 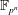$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{F}_{p^n}$ with the successive resultants algorithm

Part of: Number theory Finite fields and commutative rings (number-theoretic aspects)

Published online by Cambridge University Press:  01 August 2014

Christophe Petit
Christophe Petit*
Affiliation:
UCL Crypto Group, Université catholique de Louvain, Place du Levant 3 , B1348 Louvain-la-Neuve, Belgium email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The problem of solving polynomial equations over finite fields has many applications in cryptography and coding theory. In this paper, we consider polynomial equations over a ‘large’ finite field with a ‘small’ characteristic. We introduce a new algorithm for solving this type of equations, called the successive resultants algorithm (SRA). SRA is radically different from previous algorithms for this problem, yet it is conceptually simple. A straightforward implementation using Magma was able to beat the built-in Roots function for some parameters. These preliminary results encourage a more detailed study of SRA and its applications. Moreover, we point out that an extension of SRA to the multivariate case would have an important impact on the practical security of the elliptic curve discrete logarithm problem in the small characteristic case.

Supplementary materials are available with this article.

MSC classification

Secondary: 11-04: Explicit machine computation and programs (not the theory of computation or programming) 11T06: Polynomials 11T55: Arithmetic theory of polynomial rings over finite fields 11T71: Algebraic coding theory; cryptography
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Special Issue A: Algorithmic Number Theory Symposium XI , 2014 , pp. 203 - 217
Copyright
© The Author 2014 

References

Berlekamp, E., ‘Factoring polynomials over large finite fields’, Math. Comput. 111 (1970) 713–735.Google Scholar
Berlekamp, E. R., Algebraic coding theory (Aegean Park Press, Laguna Hills, CA, 1984).Google Scholar
Berlekamp, E. R., Rumsey, H. and Solomon, G., ‘On the solution of algebraic equations over finite fields’, Inf. Control 10 (1967) no. 6, 553–564.CrossRefGoogle Scholar
Cantor, D. G. and Zassenhaus, H., ‘A new algorithm for factoring polynomials over finite fields’, Math. Comput. 36 (1981) no. 154, 587–592.CrossRefGoogle Scholar
Chen, Y. and Nguyen, P. Q., ‘Faster algorithms for approximate common divisors: breaking fully-homomorphic-encryption challenges over the integers’, Advances in cryptology – EUROCRYPT 2012, Lecture Notes in Computer Science 7237 (eds Pointcheval, D. and Johansson, T.; Springer, 2012) 502–519.Google Scholar
Faugère, J.-C., Perret, L., Petit, C. and Guénaël, R., ‘New subexponential algorithms for factoring in $SL(2,2^n)$’, Cryptology ePrint Archive, Report 2011/598, 2011. http://eprint.iacr.org/.Google Scholar
Faugère, J.-C., Perret, L., Petit, C. and Renault, G., ‘Improving the complexity of index calculus algorithms in elliptic curves over binary fields’, Advances in cryptology – EUROCRYPT 2012, Lecture Notes in Computer Science 7237 (eds Pointcheval, D. and Johansson, T.; Springer, 2012) 27–44.CrossRefGoogle Scholar
Kaltofen, E. and Shoup, V., ‘Subquadratic-time factoring of polynomials over finite fields’, Math. Comput. 67 (1998) no. 223, 179–1197.CrossRefGoogle Scholar
Kedlaya, K. S. and Umans, C., ‘Fast polynomial factorization and modular composition’, SIAM J. Comput. 40 (2011) no. 6, 1767–1802.CrossRefGoogle Scholar
Menezes, A., van Oorschot, P. C. and Vanstone, S. A., ‘Subgroup refinement algorithms for root finding in GF(q)’, SIAM J. Comput. 21 (1992) no. 2, 228–239.CrossRefGoogle Scholar
Petit, C. and Quisquater, J.-J., ‘On polynomial systems arising from a Weil descent’, Asiacrypt, Lecture Notes in Computer Science 7658 (eds Wang, X. and Sako, K.; Springer, 2012) 451–466.Google Scholar
Rabin, M. O., ‘Probabilistic algorithms in finite fields’, SIAM J. Comput. 9 (1980) no. 2, 273–280.CrossRefGoogle Scholar
Schönhage, A. A., ‘Schnelle Berechnung von Kettenbruchentwicklungen’, Acta Inform. 1 (1971) 139–144.CrossRefGoogle Scholar
Schönhage, A., ‘Schnelle Multiplikation von Polynomen über Körpern der Charakteristik 2’, Acta Inform. 7 (1977) no. 4, 395–398.CrossRefGoogle Scholar
Thull, K. and Yap, C., A unified approach to HGCD algorithms for polynomials and integers. Manuscript. Available from http://cs.nyu.edu/cs/faculty/yap/allpapers.html/, 1990.Google Scholar
van Oorschot, P. C. and Vanstone, S. A., ‘A geometric approach to root finding in GF(qm)’, IEEE Trans. Inf. Theor. 35 (1989) no. 2, 444–453.CrossRefGoogle Scholar
von zur Gathen, J. and Gerhard, J., Modern computer algebra, 2nd edn (Cambridge University Press, 2003).Google Scholar
von zur Gathen, J. and Panario, D., ‘Factoring polynomials over finite fields: a survey’, J. Symbolic Comput. 31 (2001) no. 1/2, 3–17.CrossRefGoogle Scholar
von zur Gathen, J. and Shoup, V., ‘Computing Frobenius maps and factoring polynomials’, Comput. Complexity 2 (1992) 187–224.CrossRefGoogle Scholar
Bosma, W., Cannon, J. J., Fieker, C. and Steel, A. (eds), Handbook of Magma functions, version 2.20 (2013) http://magma.maths.usyd.edu.au/magma/.Google Scholar
Williams, V. V., ‘Multiplying matrices faster than Coppersmith-Winograd’, Proceedings of the Forty-fourth Annual ACM Symposium on Theory of Computing, STOC ’12 (eds Karloff, H. J. and Pitassi, T.; ACM, 2012) 887–898.Google Scholar