Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-20T18:36:11.677Z Has data issue: false hasContentIssue false
  • English
  • Français

Explicit computations of Serre’s obstruction for genus-3 curves and application to optimal curves

Part of: Arithmetic algebraic geometry Curves

Published online by Cambridge University Press:  01 May 2010

Christophe Ritzenthaler
Christophe Ritzenthaler*
Affiliation:
Institut de mathématiques de Luminy, UMR 6206, 163 Avenue de Luminy Case 90713288 Marseille, France (email: [email protected])

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let k be a field of characteristic other than 2. There can be an obstruction to a principally polarized abelian threefold (A,a) over k, which is a Jacobian over 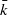, being a Jacobian over k; this can be computed in terms of the rationality of the square root of the value of a certain Siegel modular form. We show how to do this explicitly for principally polarized abelian threefolds which are the third power of an elliptic curve with complex multiplication. We use our numerical results to prove or refute the existence of some optimal curves of genus 3.

MSC classification

Secondary: 11G20: Curves over finite and local fields 14H45: Special curves and curves of low genus 14H40: Jacobians, Prym varieties
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 13 , January 2010 , pp. 192 - 207
Copyright
Copyright © London Mathematical Society 2010

References

[1] Alekseenko, E., Aleshnikov, S., Markin, N. and Zaytsev, A., ‘Optimal curves of genus 3 over finite fields with discriminant −19’, Preprint, 2009, http://arxiv.org/abs/0902.1901.Google Scholar
[2] Birkenhake, C. and Lange, H., Complex abelian varieties, 2nd edn Grundlehren der Mathematischen Wissenschaften 302 (Springer, Berlin, 2004).CrossRefGoogle Scholar
[3] Deconinck, B. and van Hoeij, M., ‘algcurves[Siegel]’, 2001,http://www.math.fsu.edu/∼hoeij/RiemannTheta/Siegel.Google Scholar
[4] Deuring, M., ‘Die Typen der Multiplicatorenringe elliptischer Funktionenkörper’, Abh. Math. Sem. Univ. Hamburg 14 (1941) 197–272.CrossRefGoogle Scholar
[5] Faltings, G. and Chai, C.-L., Degeneration of abelian varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) 22 (Springer, Berlin, 1990).CrossRefGoogle Scholar
[6] Van der Geer, G. and van der Vlugt, M., ‘Tables of curves with many points’, 2009,http://www.science.uva.nl/∼geer/.CrossRefGoogle Scholar
[7] Gross, B. H., Arithmetic on elliptic curves with complex multiplication, Lecture Notes in Mathematics 776 (Springer, Berlin, 1980).CrossRefGoogle Scholar
[8] Guàrdia, J., ‘On the Torelli problem and Jacobian Nullwerte in genus three’, Preprint, 2009,http://arxiv.org/abs/0901.4376.Google Scholar
[9] Hoffmann, D. W., ‘On positive definite hermitian forms’, Manuscripta Math. 71 (1991) 399–429.CrossRefGoogle Scholar
[10] Howe, E., Nart, E. and Ritzenthaler, C., ‘Isogeny classes of Jacobians of dimension 2 over finite fields’, Ann. Inst. Fourier (Grenoble) 59 (2009) 239–289.CrossRefGoogle Scholar
[11] Hoyt, W. L., ‘On products and algebraic families of Jacobian varieties’, Ann. of Math. 77 (1963) 415–423.CrossRefGoogle Scholar
[12] Ibukiyama, T., ‘On rational points of curves of genus 3 over finite fields’, Tôhoku Math. J. 45 (1993) 311–329.CrossRefGoogle Scholar
[13] Ichikawa, T., ‘Teichmüller modular forms of degree 3’, Amer. J. Math. 117 (1995) 1057–1061.CrossRefGoogle Scholar
[14] Ichikawa, T., ‘Theta constants and Teichmüller modular forms’, J. Number Theory 61 (1996) 409–419.CrossRefGoogle Scholar
[15] Ichikawa, T., ‘Generalized Tate curve and integral Teichmüller modular forms’, Amer. J. Math. 122 (2000) 1139–1174.CrossRefGoogle Scholar
[16] Igusa, J.-I., ‘Modular forms and projective invariants’, Amer. J. Math 89 (1967) 817–855.CrossRefGoogle Scholar
[17] Klein, F., ‘Zur Theorie der Abelschen Funktionen’, Math. Ann. 36 (1889–90); Gesammelte mathematische Abhandlungen XCVII, 388–474.Google Scholar
[18] Lachaud, G. and Ritzenthaler, C., ‘On a conjecture of Serre on abelian threefolds’, Symposium on algebraic geometry and its applications (Tahiti, 2007) (World Scientific, Singapore, 2008) 88–115.CrossRefGoogle Scholar
[19] Lachaud, G., Ritzenthaler, C. and Zykin, A., ‘Jacobians among Abelian threefolds: a formula of Klein and a question of Serre’, Math. Res. Lett., to appear.Google Scholar
[20] Lange, H., ‘Principal polarizations on products of elliptic curves’, The geometry of Riemann surfaces and abelian varieties, Contemporary Mathematics 397 (American Mathematical Society, Providence, RI, 2006) 153–162.CrossRefGoogle Scholar
[21] Lauter, K., ‘Geometric methods for improving the upper bounds on the number of rational points on algebraic curves over finite fields’, J. Algebraic Geom. 10 (2001) 19–36, with an appendix by J.-P. Serre.Google Scholar
[22] Lauter, K., ‘The maximum or minimum number of rational points on genus three curves over finite fields’, Compositio Math. 134 (2002) 87–111, with an appendix by J.-P. Serre.CrossRefGoogle Scholar
[23] Meagher, S., ‘Twists of genus three and their Jacobians’, PhD Thesis, Rijksuniversiteit Groningen, 2008, http://irs.ub.rug.nl/ppn/314417028.Google Scholar
[24] Milne, J. S., ‘Abelian varieties’, Arithmetic geometry, (eds Cornell, G. and Silverman, J. H.; Springer, New York, 1986).Google Scholar
[25] Mumford, D., Abelian varieties (Oxford University Press, Oxford, 1970).Google Scholar
[26] Nart, E. and Ritzenthaler, C., ‘Jacobians in isogeny classes of supersingular abelian threefolds in characteristic 2’, Finite Fields Appl. 14 (2008) 676–702.CrossRefGoogle Scholar
[27] Nart, E. and Ritzenthaler, C., ‘Genus 3 curves with many involutions and application to maximal curves in characteristic 2’, Proceedings of AGCT-12, to appear.Google Scholar
[28] Oort, F. and Ueno, K., ‘Principally polarized abelian varieties of dimension two or three are Jacobian varieties’, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 20 (1973) 377–381.Google Scholar
[29] Schiemann, A., ‘Classification of hermitian forms with the neighbour method’, J. Symbolic Comput. 26 (1998) 487–508. See tables at http://www.math.uni-sb.de/ag/schulze/Hermitian-lattices/.CrossRefGoogle Scholar
[30] Serre, J.-P., ‘Nombre de points des courbes algébriques sur 𝔽q’, Séminaire de Théorie des Nombres de Bordeaux, 1982–83, exp. no. 22 (Oeuvres III, no. 132, 701–705).Google Scholar
[31] Top, J., ‘Curves of genus 3 over small finite fields’, Indag. Math. (N.S.) 14 (2003) 275–283.CrossRefGoogle Scholar
[32] Waterhouse, W. C., ‘Abelian varieties over finite fields’, Ann. Sci. École Norm. Sup. (4) (1969) 521–560.CrossRefGoogle Scholar