Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T21:27:43.846Z Has data issue: false hasContentIssue false
  • English
  • Français

Explicit application of Waldspurger’s theorem

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  01 August 2013

Soma Purkait
Soma Purkait*
Affiliation:
Mathematics Institute,Zeeman Building,University of Warwick,Coventry, CV4 7AL,United Kingdom email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a given cusp form 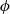$\phi $ of even integral weight satisfying certain hypotheses, Waldspurger’s theorem relates the critical value of the 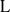$\mathrm{L} $-function of the 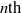$n\mathrm{th} $ quadratic twist of 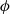$\phi $ to the 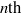$n\mathrm{th} $ coefficient of a certain modular form of half-integral weight. Waldspurger’s recipes for these modular forms of half-integral weight are far from being explicit. In particular, they are expressed in the language of automorphic representations and Hecke characters. We translate these recipes into congruence conditions involving easily computable values of Dirichlet characters. We illustrate the practicality of our ‘simplified Waldspurger’ by giving several examples.

MSC classification

Secondary: 11F37: Forms of half-integer weight; nonholomorphic modular forms 11F70: Representation-theoretic methods; automorphic representations over local and global fields 11F11: Holomorphic modular forms of integral weight
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 16 , October 2013 , pp. 216 - 245
Copyright
© The Author(s) 2013 

References

Atkin, A. O. L. and Li, W., ‘Twists of newforms and pseudo-eigenvalues of $W$ -operators’, Invent. Math. 48 (1978) 221–243.CrossRefGoogle Scholar
Baruch, E. and Mao, Z., ‘Central value of automorphic L-functions’, Geom. Funct. Anal. 17 (2007) 333–384.CrossRefGoogle Scholar
Basmaji, J., ‘Ein Algorithmus zur Berechnung von Hecke-Operatoren und Anwendungen auf modulare Kurven’, PhD Dissertation, Universität Gesamthochschule Essen, März, 1996.Google Scholar
Böcherer, S. and Schulze-Pillot, R., ‘Vector valued theta series and Waldspurger’s theorem’, Abh. Math. Semin. Univ. Hambg. 64 (1994) 211–233.CrossRefGoogle Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The magma algebra system I: the user language’, J. Symbolic Comput. 24 (1997) 235–265; see also http://magma.maths.usyd.edu.au/magma/.CrossRefGoogle Scholar
Bump, D., Automorphic forms and representations, Cambridge Studies in Advanced Mathematics 55 (Cambridge University Press, 1996).Google Scholar
Bungert, M., ‘Construction of a cuspform of weight 3/2’, Arch. Math. 60 (1993) 530–534.CrossRefGoogle Scholar
Cohn, H., A classical invitation to algebraic numbers and class fields (Springer, 1980).Google Scholar
Connell, I., ‘Calculating root numbers of elliptic curves over $ \mathbb{Q} $ ’, Manuscripta Math. 82 (1994) 93–104.CrossRefGoogle Scholar
Dickson, L. E., Studies in the theory of numbers (The University of Chicago Press, Chicago, IL, 1930).Google Scholar
Flicker, Y., ‘Automorphic forms on covering groups of GL(2)’, Invent. Math. 57 (1980) 119–182.CrossRefGoogle Scholar
Hamieh, A., ‘Ternary quadratic forms and half-integral weight modular forms’, LMS J. Comput. Math. 15 (2012) 418–435.CrossRefGoogle Scholar
Katz, N., ‘Galois properties of torsion points on Abelian varieties’, Invent. Math. 62 (1981) 481–502.CrossRefGoogle Scholar
Koblitz, N., Introduction to elliptic curves and modular forms, Graduate Texts in Mathematics 97 (Springer, 1993).CrossRefGoogle Scholar
Kohnen, W., ‘Newforms of half-integral weight’, J. reine angew. Math. 333 (1982) 32–72.Google Scholar
Larry Lehman, J., ‘Levels of positive definite ternary quadratic forms’, Math. Comp. 58 (1992) 399–417.CrossRefGoogle Scholar
Mao, Z., ‘A generalized Shimura correspondence for newforms’, J. Number Theory 128 (2008) 71–95.CrossRefGoogle Scholar
Purkait, S., ‘On Shimura’s decomposition’, Int. J. Number Theory, to appear, doi:10.1142/S179304211350036X.CrossRefGoogle Scholar
Siegel, C. L., Über die analytische Theorie der quadratischen Formen, Gesammelte Abhandlungen 1 (Springer, Berlin, 1966) 326–405.Google Scholar
Serre, J. P., A course in arithmetic, Graduate Texts in Mathematics 7 (Springer, 1973).CrossRefGoogle Scholar
Shimura, G., ‘On Modular forms of half integral weight’, Ann. of Math. (2) 97 (1973) 440–481.CrossRefGoogle Scholar
Shimura, G., ‘The critical values of certain zeta functions associated with modular forms of half-integral weight’, J. Math. Soc. Japan 33 (1981) 649–672.CrossRefGoogle Scholar
Silverman, J. H., The arithmetic of elliptic curves, Graduate Texts in Mathematics 106 (Springer, 1986).CrossRefGoogle Scholar
Silverman, J. H., Advanced topics in the arithmetic of elliptic curves, Graduate Texts in Mathematics 151 (Springer, 1994).CrossRefGoogle Scholar
Sturm, J., ‘On the congruence of modular forms’, Number theory (New York, 1984–1985), Lecture Notes in Mathematics 1240 (Springer, Berlin, 1987) 275–280.Google Scholar
Tate, J., ‘Fourier analysis in number fields and Hecke’s zeta-functions’, Algebraic number theory, (eds Cassels, J. W. S. and Fröhlich, A.; Academic Press, 1967) 305–347.Google Scholar
Tate, J., ‘Number theoretic background’, Automorphic forms, representations, and L-functions, Proc. Sympos. Pure Math. XXXIII 2 (1979) 3–26.CrossRefGoogle Scholar
Tunnell, J. B., ‘A classical Diophantine problem and modular forms of weight 3/2’, Invent. Math. 72 (1983) 323–334.CrossRefGoogle Scholar
Vigneras, M. F., ‘Valeur au centre de symétrie des functions L associées aux formes modulaires’, Séminaire de Théorie de Nombres, Paris, 1979–1980, Progress in Mathematics 12 (Birkhäuser, Boston, MA, 1981) 331–356.Google Scholar
Waldspurger, J. L., ‘Sur les coefficients de Fourier des formes modulaires de poids demi-entier’, J. Math. Pures Appl. 60 (1981) 375–484.Google Scholar
Yoshida, S., ‘Some variants of the congruent number probelm II’, Kyushu J. Math. 56 (2002) 147–165.CrossRefGoogle Scholar