Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-14T01:32:10.218Z Has data issue: false hasContentIssue false
  • English
  • Français

Congruence testing for odd subgroups of the modular group

Part of: Other groups of matrices

Published online by Cambridge University Press:  01 May 2014

Thomas Hamilton  and
David Loeffler
Thomas Hamilton
Affiliation:
Premier Pensions Management Corinthian House 17 Lansdowne Road Croydon CR0 2BXUnited Kingdom
David Loeffler
Affiliation:
Mathematics Institute University of Warwick Coventry CV4 7ALUnited Kingdom email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a computationally effective criterion for determining whether a finite-index subgroup of 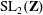$\mathrm{SL}_2(\mathbf{Z})$ is a congruence subgroup, extending earlier work of Hsu for subgroups of 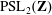$\mathrm{PSL}_2(\mathbf{Z})$.

MSC classification

Secondary: 20H05: Unimodular groups, congruence subgroups
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Issue 1 , 2014 , pp. 206 - 208
Copyright
© The Author(s) 2014 

References

Behr, H. and Mennicke, J., ‘A presentation of the groups PSL(2, p)’, Canad. J. Math. 20 (1968) 1432–1438; MR 0236269.CrossRefGoogle Scholar
Hsu, T., ‘Identifying congruence subgroups of the modular group’, Proc. Amer. Math. Soc. 124 (1996) 1351–1359; MR 1343700.CrossRefGoogle Scholar
Kiming, I., Schütt, M. and Verrill, H. A., ‘Lifts of projective congruence groups’, J. Lond. Math. Soc. (2) 83 (2011) 96–120; MR 2763946.CrossRefGoogle Scholar