Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T11:08:54.482Z Has data issue: false hasContentIssue false
  • English
  • Français

A computational iterative method for solving nonlinear ordinary differential equations

Part of: General higher-order equations and systems Numerical analysis: Ordinary differential equations

Published online by Cambridge University Press:  01 December 2015

H. Temimi  and
A. R. Ansari
H. Temimi
Affiliation:
Department of Mathematics & Natural Sciences, Gulf University for Science & Technology, P.O. Box 7207, Hawally 32093, Kuwait email [email protected]
A. R. Ansari
Affiliation:
Department of Mathematics & Natural Sciences, Gulf University for Science & Technology, P.O. Box 7207, Hawally 32093, Kuwait email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

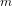We present a quasi-linear iterative method for solving a system of $m$-nonlinear coupled differential equations. We provide an error analysis of the method to study its convergence criteria. In order to show the efficiency of the method, we consider some computational examples of this class of problem. These examples validate the accuracy of the method and show that it gives results which are convergent to the exact solutions. We prove that the method is accurate, fast and has a reasonable rate of convergence by computing some local and global error indicators.

MSC classification

Primary: 65L10: Boundary value problems 35G30: Boundary value problems for nonlinear higher-order equations
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 18 , Issue 1 , 2015 , pp. 730 - 753
Copyright
© The Author(s) 2015 

References

Bellman, R. E. and Kalaba, R. E., Quasilinearisation and nonlinear boundary-value problems (Elsevier, New York, 1965).Google Scholar
He, J. H., ‘Iteration perturbation method for strongly nonlinear oscillations’, J. Vib. Control 2 (2002) 121–126.Google Scholar
Herisanu, N. and Marinca, V., ‘An iteration procedure with application to van der pol oscillator’, Int. J. Nonlinear Sci. Numer. Simul. 10 (2009) 353–361.Google Scholar
Huang, Y.-J. and Liu, H.-K., ‘A new modification of the variational iteration method for van der Pol equations’, Appl. Math. Model. 37 (2013) 8118–8130.CrossRefGoogle Scholar
Li, P. S. and Wu, B. S., ‘An iteration approach to nonlinear oscillations of conservative single-degree of freedom systems’, Acta Mech. 170 (2004) 69–75.CrossRefGoogle Scholar
Liao, S. J., Beyond perturbation: introduction to homotopy analysis method (Chapman & Hall/CRC, 2003).Google Scholar
Liao, S. J., ‘Notes on the homotopy analysis method: some definitions and theorems’, Commun. Nonlinear Sci. Numer. Simul. 14 (2009) 983–997.CrossRefGoogle Scholar
Liao, S. J. and Chwang, A. T., ‘Application of homotopy analysis method in nonlinear oscillations’, J. Appl. Mech. 65 (1998) 914–922.Google Scholar
Marinca, V. and Herianu, N., ‘Optimal parametric iteration method for solving multispecies Lotka–Volterra equations’, Discrete Dyn. Nat. Soc. 2012 (2012) Article ID 842121, doi:10.1155/2012/842121.Google Scholar
Mickens, R. E., ‘Iteration procedure for determining approximate solutions to nonlinear oscillation equation’, J. Sound Vib. 116 (1987) 185–188.Google Scholar
Temimi, H. and Ansari, A. R., ‘A semi-analytical iterative technique for solving nonlinear problems’, Comput. Math. Appl. 61 (2011) 203–210.CrossRefGoogle Scholar
Temimi, H. and Ansari, A. R., ‘A new iterative technique for solving nonlinear second order multi-point boundary value problems’, Appl. Math. Comput. 218 (2011) 1457–1466.Google Scholar