Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T21:28:45.615Z Has data issue: false hasContentIssue false
  • English
  • Français

Class number calculation using Siegel functions

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  01 August 2014

T. Fukuda  and
K. Komatsu
T. Fukuda
Affiliation:
Department of Mathematics, College of Industrial Technology, Nihon University, 2-11-1 Shin-ei, Narashino, Chiba 275-8576, Japan email [email protected]
K. Komatsu
Affiliation:
Department of Mathematical Science, School of Science and Engineering, Waseda University, 3-4-1 Okubo, Shinjuku, Tokyo 169-8555, Japan email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We propose a fast method of calculating the 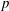$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-part of the class numbers in certain non-cyclotomic 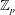$\mathbb{Z}_p$-extensions of an imaginary quadratic field using elliptic units constructed by Siegel functions. We carried out practical calculations for 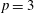$p=3$ and determined 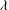$\lambda $-invariants of such 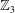$\mathbb{Z}_3$-extensions which were not known in our previous paper.

MSC classification

Secondary: 11R29: Class numbers, class groups, discriminants 11R23: Iwasawa theory
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Special Issue A: Algorithmic Number Theory Symposium XI , 2014 , pp. 295 - 302
Copyright
© The Author(s) 2014 

References

Cohen, H., Advanced topics in computational number theory, Graduate Texts in Mathematics 193 (Springer, Berlin, 2000).CrossRefGoogle Scholar
Fukuda, T., ‘Remarks on ℤp-extensions of number fields’, Proc. Japan Acad. Ser. A Math. Sci. 65 (1989) 260–262.Google Scholar
Fukuda, T. and Komatsu, K., ‘Non-cyclotomic ℤp-extensions of imaginary quadratic fields’, Exp. Math. 11 (2002) 469–475.CrossRefGoogle Scholar
Gillard, R., ‘Fonctions L p-adiques des corps quadratiques imaginaires et de leurs extensions abéliennes’, J. reine angew. Math. 358 (1985) 76–91.Google Scholar
Kubert, D. S. and Lang, S., Modular units, Grundlehren der Mathematischen Wissenschaften 244 (Springer, 1981).CrossRefGoogle Scholar
Pohst, M. E., ‘Computing invariants of algebraic number fields’, Group theory, algebra, and number theory (ed. Zimmer, H. G.; de Gruyter, 1996) 53–73.CrossRefGoogle Scholar
Schneps, L., ‘On the μ-invariant of p-adic L-functions attached to elliptic curves with complex multiplication’, J. Number Theory 25 (1987) 20–33.CrossRefGoogle Scholar