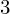Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T07:36:07.158Z Has data issue: false hasContentIssue false
  • English
  • Français

A census of zeta functions of quartic K$3$ surfaces over 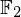$\mathbb{F}_{2}$

Part of: Zeta and $L$-functions: analytic theory Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  26 August 2016

Kiran S. Kedlaya  and
Andrew V. Sutherland
Kiran S. Kedlaya
Affiliation:
Department of Mathematics, University of California, San Diego, 9500 Gilman Drive #0112, La Jolla, CA 92093, USA email [email protected]
Andrew V. Sutherland
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We compute the complete set of candidates for the zeta function of a K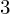$3$ surface over 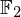$\mathbb{F}_{2}$ consistent with the Weil and Tate conjectures, as well as the complete set of zeta functions of smooth quartic surfaces over 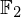$\mathbb{F}_{2}$. These sets differ substantially, but we do identify natural subsets which coincide. This gives some numerical evidence towards a Honda–Tate theorem for transcendental zeta functions of K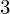$3$ surfaces; such a result would refine a recent theorem of Taelman, in which one must allow an uncontrolled base field extension.

MSC classification

Primary: 11M38: Zeta and $L$-functions in characteristic $p$ 14J28: $K3$ surfaces and Enriques surfaces
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 1 - 11
Copyright
© The Author(s) 2016 

References

Abbott, T. G., Kedlaya, K. S. and Roe, D., ‘Bounding Picard numbers of surfaces using p-adic cohomology’, Arithmetic, geometry and coding theory (AGCT 2005) , Séminaires et Congrès 21 (Société Mathématique de France, Paris, 2009) 125–159.Google Scholar
Basu, S., Pollack, R. and Roy, M.-F., Algorithms in real algebraic geometry , 2nd edn, Algorithms and Computation in Mathematics 10 (Springer, Berlin, 2006).Google Scholar
Berlekamp, E. R., ‘Factoring polynomials over finite fields’, Bell Syst. Tech. J. 46 (1967) 1853–1859.Google Scholar
Cohen, H., A course in computational algebraic number theory, 3rd printing (Springer, Berlin, 1996).Google Scholar
Costa, E. and Tschinkel, Y., ‘Variation of Néron–Severi ranks of reductions of K3 surfaces’, Exp. Math. 23 (2014) 475–481.Google Scholar
Cython – C-extensions for Python, version 0.24, 2016, http://cython.org.Google Scholar
Elsenhans, A.-S. and Jahnel, J., ‘On Weil polynomials of K3 surfaces’, ANTS-XI: Algorithmic Number Theory Symposium , Lecture Notes in Computational Science 6197 (Springer, Berlin, 2010).Google Scholar
Gritsenko, V. A., Hulek, K. and Sankaran, G. K., ‘The Kodaira dimension of the moduli of K3 surfaces’, Invent. Math. 169 (2007) 519–567.Google Scholar
Haloui, S., ‘The characteristic polynomials of abelian varieties of dimension 3 over finite fields’, J. Number Theory 130 (2010) 2745–2752.Google Scholar
Hart, W., Johansson, F. and Pancratz, S., ‘FLINT: Fast Library for Number Theory, version 2.4.5’, 2015, http://flintlib.org.Google Scholar
Honda, T., ‘Isogeny classes of abelian varieties over finite fields’, J. Math. Soc. Japan 20 (1968) 83–95.Google Scholar
Huybrechts, D., Lectures on K3 surfaces (Cambridge University Press, Cambridge, 2015).Google Scholar
Kedlaya, K. S., ‘Search techniques for root-unitary polynomials’, Computational arithmetic geometry , Contemporary Mathematics 463 (American Mathematical Society, Providence, RI, 2008) 71–82; Associated code available at http://kskedlaya.org/papers/.Google Scholar
Kim, W. and Madapusi Pera, K., ‘2-adic integral canonical models and the Tate conjecture in characteristic 2’, Preprint, 2015, arXiv:1512.02540v1.Google Scholar
Lieblich, M. and Olsson, M., ‘Fourier–Mukai partners of K3-surfaces in positive characteristic’, Ann. Sci. Éc. Norm. Supér. (4) 48 (2015) 1001–1033.Google Scholar
Liedtke, C. and Matsumuto, Y., ‘Good reduction of K $3$ surfaces’, Preprint, 2015, arXiv:1411.4797v2.Google Scholar
Madapusi Pera, K., ‘The Tate conjecture for K3 surfaces in odd characteristic’, Invent. Math. 201 (2015) 625–668.Google Scholar
Malle, G., ‘The totally real primitive number fields of discriminant at most 109 ’, Algorithmic number theory (ANTS-VII) , Lecture Notes in Computational Science 4076 (Springer, Berlin, 2006) 114–123.CrossRefGoogle Scholar
Milne, J. and Waterhouse, W., ‘Abelian varieties over finite fields’, 1969 Number theory institute , Proceedings of Symposia in Pure Mathematics 20 (American Mathematical Society, Providence, RI, 1971) 53–64.Google Scholar
Osserman, B., ‘The Weil conjectures’, The Princeton companion to mathematics (Princeton University Press, Princeton, NJ, 2008) 729–732.Google Scholar
The PARI Group, ‘PARI/GP version 2.7.0’, 2014, http://pari.math.u-bordeaux.fr/.Google Scholar
Sage version 6.7, 2015, http://www.sagemath.org/.Google Scholar
Taelman, L., ‘K $3$ surfaces over finite fields with given L-function’, Algebra Number Theory, to appear, Preprint, 2015, arXiv:1507.08547v2.CrossRefGoogle Scholar
Tate, J., ‘Endomorphisms of abelian varieties over finite fields’, Invent. Math. 2 (1966) 134–144.CrossRefGoogle Scholar
van der Geer, G., Howe, E. W., Lauter, K. E. and Ritzenthaler, C., Tables of curves with many points, 2009, http://www.manypoints.org [accessed 19 July 2016].Google Scholar
Voight, J., ‘Enumeration of totally real number fields of bounded root discriminant’, Algorithmic number theory (ANTS-VIII) , Lecture Notes in Computational Science 5011 (Springer, Berlin, 2008) 268–281.Google Scholar
Zinoviev, V., ‘On the solutions of equations of degree’, Research Report RR-2829, INRIA, 1996, available at http://hal.inria.fr/inria-00073862.Google Scholar