Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T02:17:53.941Z Has data issue: false hasContentIssue false
  • English
  • Français

A census of quadratic post-critically finite rational functions defined over 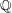$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Q}$

Part of: Computational number theory Arithmetic and non-Archimedean dynamical systems Algebraic number theory: global fields

Published online by Cambridge University Press:  01 July 2014

David Lukas ,
Michelle Manes  and
Diane Yap
David Lukas
Affiliation:
University of Hawaii, Honolulu, HI 96822,USA email [email protected]
Michelle Manes
Affiliation:
Department of Mathematics, University of Hawaii, Honolulu, HI 96822,USA email [email protected]
Diane Yap
Affiliation:
Department of Mathematics, University of Hawaii, Honolulu, HI 96822,USA email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We find all quadratic post-critically finite (PCF) rational functions defined over 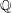$\mathbb{Q}$, up to conjugation by elements of 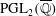$\mathop{\rm PGL}_2(\overline{\mathbb{Q}})$. We describe an algorithm to search for possibly PCF functions. Using the algorithm, we eliminate all but 12 rational functions, all of which are verified to be PCF. We also give a complete description of all possible rational preperiodic structures for quadratic PCF functions defined over 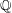$\mathbb{Q}$.

MSC classification

Secondary: 37P05: Polynomial and rational maps 37P15: Global ground fields 11R99: None of the above, but in this section 11Y99: None of the above, but in this section
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Special Issue A: Algorithmic Number Theory Symposium XI , 2014 , pp. 314 - 329
Copyright
© The Author(s) 2014 

References

Benedetto, R., Ingram, P., Jones, R. and Levy, A., ‘Critical orbits and attracting cycles in $p$-adic dynamics’, Preprint, 2012, arXiv:1201.1605v1.Google Scholar
Brezin, E., Byrne, R., Levy, J., Pilgrim, K. and Plummer, K., ‘A census of rational maps’, Conform. Geom. Dyn. 4 (2000) 35–74.CrossRefGoogle Scholar
Faber, X., ‘Rational functions with a unique critical point’, Int. Math. Res. Not. IMRN (2014) no. 3, 681–699.CrossRefGoogle Scholar
Granlund, T. et al. , GNU Multiple Precision Arithmetic Library (Version 5.1.3), Free Software Foundation, Inc., 2013, http://www.gmplib.org/.Google Scholar
Jones, R. and Manes, M., ‘Galois theory of quadratic rational functions’, Preprint, 2011,arXiv:1101.4339v3.Google Scholar
Manes, M., ‘ℚ-rational cycles for degree-2 rational maps having an automorphism’, Proc. Lond. Math. Soc. (3) 96 (2008) no. 3, 669–696.CrossRefGoogle Scholar
Manes, M., ‘Moduli spaces for families of rational maps on ℙ1’, J. Number Theory 129 (2009) no. 7, 1623–1663.CrossRefGoogle Scholar
Manes, M. and Yasufuku, Y., ‘Explicit descriptions of quadratic maps on ℙ1 defined over a field K’, Acta Arith. 148 (2011) no. 3, 257–267.CrossRefGoogle Scholar
Milnor, J., ‘Geometry and dynamics of quadratic rational maps’, Experiment. Math. 2 (1993) no. 1, 37–83.CrossRefGoogle Scholar
Nelson, P., Downs, J. and Poznyakoff, S., GNU gdbm (Version 1.10), Free Software Foundation, Inc., 2011, http://www.gnu.org/software/gdbm/.Google Scholar
Olson, L. D., ‘Points of finite order on elliptic curves with complex multiplication’, Manuscripta Math. 14 (1974) 195–205.CrossRefGoogle Scholar
Poonen, B., ‘The classification of rational preperiodic points of quadratic polynomials over ℚ: a refined conjecture’, Math. Z. 228 (1998) no. 1, 11–29.CrossRefGoogle Scholar
Silverman, J. H., The arithmetic of dynamical systems, Graduate Texts in Mathematics 241 (Springer, 2007).CrossRefGoogle Scholar
Silverman, J. H., Moduli spaces and arithmetic dynamics, CRM Monograph Series 30 (American Mathematical Society, Providence, RI, 2012).CrossRefGoogle Scholar
Stein, W. A. et al. , Sage Mathematics Software (Version 5.12). The Sage Development Team, 2013, http://www.sagemath.org.Google Scholar